[논문리뷰] VGGT: Visual Geometry Grounded Transformer
CVPR 2025 (Best Paper)
Jianyuan Wang, Minghao Chen, Nikita Karaev, Andrea Vedaldi, Christian Rupprecht, David Novotny
14 Mar 2025
[paper]
preliminary
Structure from Motion(SfM)
특정 장면을 다른 시점에서 촬영한 여러 이미지를 통해 카메라 파라미터(위치와 각도)를 추정하고, 희소한 3D point cloud를 재구성하는 기술을 의미한다. 전통적인 SfM은 다음과 같은 단계로 구성된다.
-
image matching : 서로 다른 시점의 이미지들에서 같은 지점을 찾는 과정으로, 각 이미지의 keypoint를 추출하고 이를 설명하는 벡터를 비교해 대응쌍을 만드는 과정을 의미한다.
-
triangulation : image matching을 통해 찾은 keypoint와 카메라 위치정보를 활용해 keypoint의 실제 3D 좌표를 얻어내는 과정. 실제로는 카메라에서 쏜 ray들이 만나는 지점을 찾는다.
-
bundle adjustmen : 추정된 카메라 파라미터와 3D keypoint를 동시에 최적화하여 오차를 최소화하는 과정
가장 대표적인 SfM 프레임워크로 COLMAP이 있으며, 이 또한 전통적인 SfM에 해당한다. 최근에는 딥러닝이 SfM 파이프라인에 쓰이고 있으며 end to end 미분가능 SfM인 VGGSfM가 전통적인 방법보다 좋은 성능을 보이고 있다.
Multi-view Stereo(MVS)
SfM을 통해 카메라 파라미터와 희소한 point cloud를 얻었다면, 여러장의 이미지로부터 scene을 dense하게 재구성하는 기술이다. MVS는 3가지 카테고리로 나눠진다. traditional handcrafted, global optimization, learning-based 방식이 이에 해당한다.
이중에서 learning-based 방식은 최근 큰 발전을 이루었다. 대표적으로 DUSt3R와 MASt3R이 있으며 기존의 MVS와 다르게 카메라 파라미터 없이 몇장의 사진만으로 dense point cloud를 만들어낼 수 있다.
Tracking-Any-Point
비디오에서 관심있는 포인트의 2D 대응점을 모든 프레임에 걸쳐 추적화는 태스크를 말한다. Particle Video에서 처음소개 되어 최근 딥러닝 시대에 들어 PIPs라는 기술이 각광받았다. VGGT는 해당 태스크에 특화된 모델은 아니지만 VGGT에서 추출한 feature를 기존 방법과 같이 사용시 SOTA를 찍었다고 한다.
Methodology
Overview
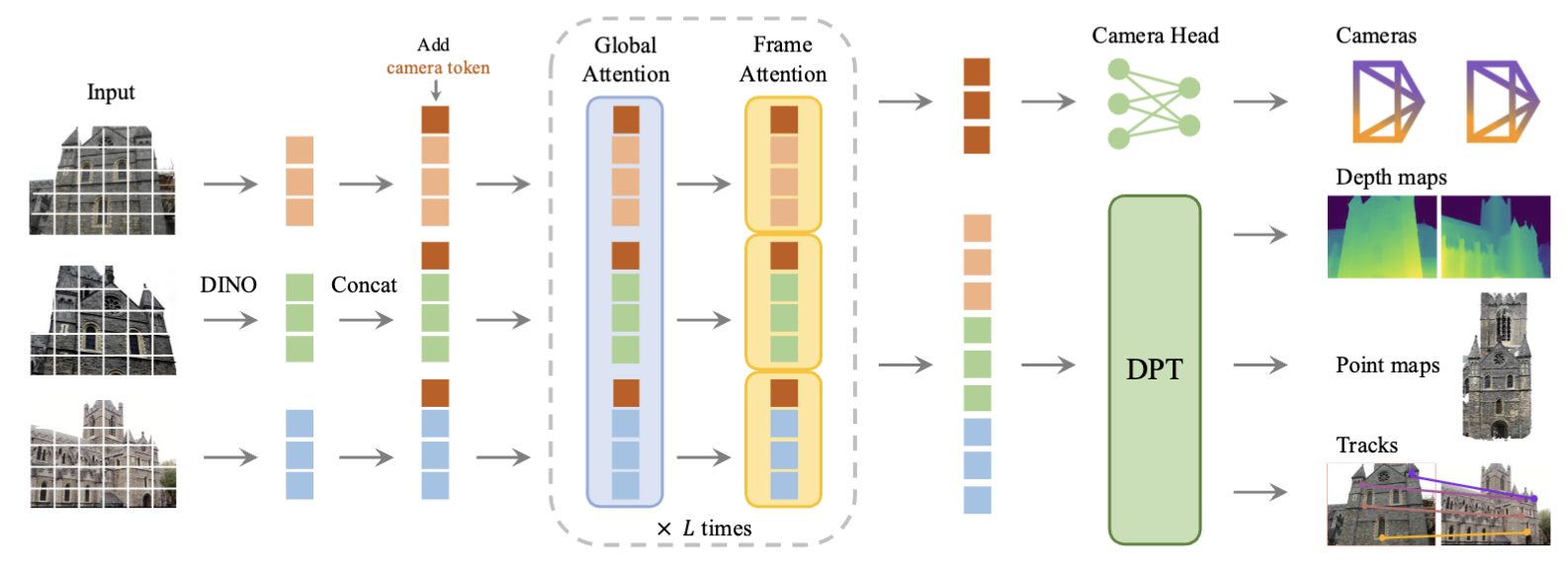
VGGT의 전체적인 흐름을 나타내는 figure이다. 해당 이미지는 VGGT로 추론할 때의 예시인데, 미리 학습된 모델에 input으로 DINO를 이용해 만들어진 토큰에 카메라 토큰을 넣어서 AA Attention 모듈에 집어 넣는다. 카메라는 Self Attention과 Linear 레이어를 지난 후에 예측되면 나머지는 DPT 모듈을 지나서 옝측하게 된다.
Problem definition and notation
\[f\left(\left(\left(I_i\right)_{i=1}^N\right)\right) = \left(\mathbf{g}_i, D_i, P_i, T_i\right)_{i=1}^N\]VGGT는 같은 3D scene을 다른 시점에서 바라본 N장의 시퀀스를 입력받는다.이때 $I_i \in \mathbb{R}^{3 \times H \times W}$인 이미지를 입력받아 위 수식과 같이 4개의 파라미터를 출력하게 된다.
- 카메라 파라미터 ($g_{i} \in \mathbf{R}^{9}$)
- 카메라 내부와 외부의 파라미터를 의미
- 회전 쿼터니언(rotation quaternion) $q \in \mathbb{R}^{4}$
- 평행 이동 벡터(translation vector) $t \in \mathbb{R}^{3}$
- 시야각(field of view) $f \in \mathbb{R}^{2}$
- 위 파라미터들의 concatenation로 구성($g=[q,t,f]$)
- depth map ($D_{i} \in \mathbb{R}^{H \times W}$)
- 이미지의 각 픽셀 위치 $y \in H \times W$가 i번째 카메라에서 관측된 깊이 $D_{i}(y)$를 매핑
- 즉 해당 카메라에서 해당 픽셀까지의 거리를 나타내는 2D 이미지
- point map ($P_{i} \in \mathbb{R}^{3 \times H \times W}$)
- 각 픽셀에 대응되는 3D상의 좌표
- 첫번째 카메라가 기준좌표가 되어 viewpoint invariant가 됨
- keypoint tracking ($T_{i} \in \mathbb{R}^{C \times H \times W}$)
- 특정 이미지의 point가 다른 이미지의 어떤 부분에 대응되는지를 담고 있는 고차원 데이터
- 특정 사진의 point를 추적하기 위해 다른 이미지를 찾아볼 때 사용할 매칭정보가 담겨진 feature
- 별도의 트래킹 모듈이 이를 넘겨받아 다른 이미지의 어디에 위치하는지 계산하게 됨
여기서 첫번째 이미지가 point map에서 reference fram이 된다는 점을 빼면, 그 외의 이미지들은 permutation equivariant하게 된다.
또한 여기서 VGGT가 예측하는 4가지 요소들은 서로 수학적으로 독립적이지 않다. 구체적으로는 point map을 통해서 카메라 파라미터를 계산하거나, depth map을 point map과 카메라 파라미터로 계산할 수 있다. 하지만 이렇게 중복된 요소를 예측하는 이유는 학습과정에서 중복된 요소을 넣는게 학습과정에서 더 성능이 잘나왔으며, 추론 단계에서도 단순히 모델이 출력한 point map 결과가 아닌 depth map과 카메라 파라미터를 통해 계산한 결과가 성능이 더 좋았기에 수학적으로는 중복되는 요소들을 모델의 출력으로 두는 것이다.
Feature Backbone
VGGT는 3D를 위해 복잡한 특수 구조를 사용하는 대신, 최소한의 inductive bias을 가진 단순한 구조를 채택한다. 그리고 대규모의 3D annotated data를 통해 모델이 스스로 학습하도록 하고, 이는 LLM에서 사용되던 large transformer 방식이라고 저자들은 주장한다.
먼저 입력된 각 이미지는 DINO 모델을 통해 작은 패치가 되고, 이 토큰들의 집합을 main network인 alternating attention 네트워크에 집어넣게 된다.alternating attention는 일반적인 트랜스포머에서 구조를 바꾼 네트워크로서 Frame-wise Self-Attention와 Global Self-Attention를 번갈아 가며 수행하는 방식을 의미한다.
-
Frame-wise Self-Attention : 각 이미지 내부의 토큰끼리만 상호작용하여 이미지 내 정보를 처리 및 activation을 정규화하는 역할을 하게된다.
-
Global Self-Attention : 모든 이미지(프레임)의 모든 토큰이 상호작용하여 서로 다른 이미지 간 정보를 통합한다.
이 두 Attention을 번갈아가며 반복함으로서 개별 이미지 특징을 유지하면서 이미지 사이의 관계를 효과적으로 학습할 수 있게 된다. 여기서 기본값으로 두 attention층을 포함해 24층을 적용했으며, cross attention 없이 self attention 만을 적용하였다.
Prediction heads
해당 파트에서는 사전 학습된 Feature Backbone으로 어떻게 위에 언급한 4가지 요소를 예측하는지를 다루고 있다. 여기에서 각 이미지의 토큰에 더불어 후에 카메라 파라미터의 정보를 담기 위한 1개의 카메라 토큰과 alternating attention에서 임시 메모리처럼 사용될 레지스터 토큰 4개를 더 붙여 모델에 집어넣는다. 이때 레지스터 토큰은 트랜스포머의 복잡한 연산을 돕고, 계산이 끝나면 버려지게 된다.
여기서 중요한 점은 첫번째 이미지에 들어가는 카메라 토큰과 레지스터 토큰은 다른 이미지들의 토큰들과 구별된다. 이는 모델에게 첫번째 카메라를 기준으로 다른 카메라의 상대적 위치를 알 수 있게 해준다.
여기서 위 점 덕분에 첫번째 카메라를 기준으로 나오는 모든 결과가 identity, 즉 항등하게 된다. 첫 rotation quaternion은 [0,0,0,1], translation vector는 [0,0,0]으로 고정된다.
Camera Predictions
카메라 파라미터는 카메라 토큰의 결과를 바로 출력하는게 아닌, 추가적인 4개의 self attion layer와 linear layer를 지나서 예측된다. 이를 통해 camera intrinsics와 extrinsics를 예측하게 된다.
여기서 extrinsics는 카메라의 Translation(위치)와 Rotation(방향)를 의미하고, intrinsics는 초점거리나 주점 비대칭 계수 등을 의미한다.
Dense Predictions
image token의 결과물은 depth map, point map, tracking feature를 계산하는데 사용된다. 여기서 DPT layer를 거쳐 Dense feature map으로 변환하고, 이 feature map은 3x3 Conv Layer를 지나 최종 결과물이 나오게 된다. 그리고 단순 값만 예측하는 것이 아닌 aleatoric uncertainty 즉 예측한 값이 얼마나 확실한지를 나타내는 값을 함께 출력하여 loss function에 활용하여 모델이 예측의 confidence을 출력할 때 사용된다.
DPT는 Dense Prediction Transformer의 약자로, 트랜스포머 아키텍처를 세그멘테이션 혹은 depth estimation과 같은 dense prediction에 쓰이기 위해 고안된 구조이다. 이때 DPT 모듈은 tracking의 입력으로도 쓰이게 된다.
Tracking
해당 부분은 이 사진의 point가 다른 사진의 어떤 위치에 있는지 찾기 위한 과정으로, CoTracker2라는 아키텍처를 사용한다. 특정 이미지의 특정 point를 지정하면, 그 이미지의 tracking feature에서 그 점의 feature를 뽑아와 다른 이미지의 map과 비교하여 correlation maps를 얻게된다. 이 map들을 self attention 레이어에 넣어 다른 이미지의 2D point를 구할 수 있게 된다.
여기서 신기한 점은 VGGSfM처럼 시간적 (프레임) 정보 없이 video가 아님에도 예측할 수 있다는 점이다.
Training Loss
\[\mathcal{L} = \mathcal{L}_{\text{camera}} + \mathcal{L}_{\text{depth}} + \mathcal{L}_{\text{pmap}} + \lambda \mathcal{L}_{\text{track}}\]학습을 할때 camera, depth, point map의 loss는 예측과 실제값을 비교해 loss를 구한다. 이때 트래킹만 값의 크기가 달라 0.05정도의 작은 수로 스케일링하여 loss를 더해준다.
\[\mathcal{L}_{camera} = \sum_{i=1}^{N} ||\hat{g}_i - g_i||_{\epsilon}\]camera는 Huber Loss(오차가 작을때는 L2, 오차가 클때는 L1을 사용해 이상치에 덜 민감하게 하는것)을 사용한다.
\[\mathcal{L}_{depth} = \sum_{i=1}^{N} \left( ||\Sigma_{i}^{D} \odot (\hat{D}_{i} - D_{i})||_1 + ||\Sigma_{i}^{D} \odot (\nabla\hat{D}_{i} - \nabla D_{i})||_1 - \alpha \log \Sigma_{i}^{D} \right)\]depth는 DUSt3R의 방식을 따라 Aleatoric Uncertainty 개념을 적용해 실제 값 뿐만 아니라 불확실성 맵($\Sigma_i^D$)을 고려한다. 또한 DUSt3R와 다르게 값 뿐만 아니라 gradient 항을 추가한다.
point map 손실의 경우 depth와 동일하게 실제값, 불확실성, gradient을 모두 고려하여 손실에 반영한다.
tracking의 경우 이미지의 한 점이 다른 이미지의 어디로 이동했는지를 정확히 맞췄는지 보고 판단한다. 이때 예측한 좌표와 정답 좌표 사이의 거리를 합산하고, CoTracker2의 방식에 따라 점이 가려졌는지 맞추는 Binary Cross-Entropy도 포함된다.
Ground Truth Coordinate Normalization
3D 공간을 학습할 때 ambiguity를 없애기 위해 Ground Truth Coordinate Normalization를 도입한다. 3D Scene은 확대하거나 옮기더라도 2D상에서 같아보일 수 있기 때문에, 모든 데이터를 첫번째 카메라 좌표계 기준으로 변환하여 사용한다. 이때 DUSt3R에서는 모델의 예측값을 정규화하는 대신, ground truth자체를 정규화하여 모델이 이 값을 출력하도록 학습시킨다.
Experiments
4개의 출력 파라미터의 결과
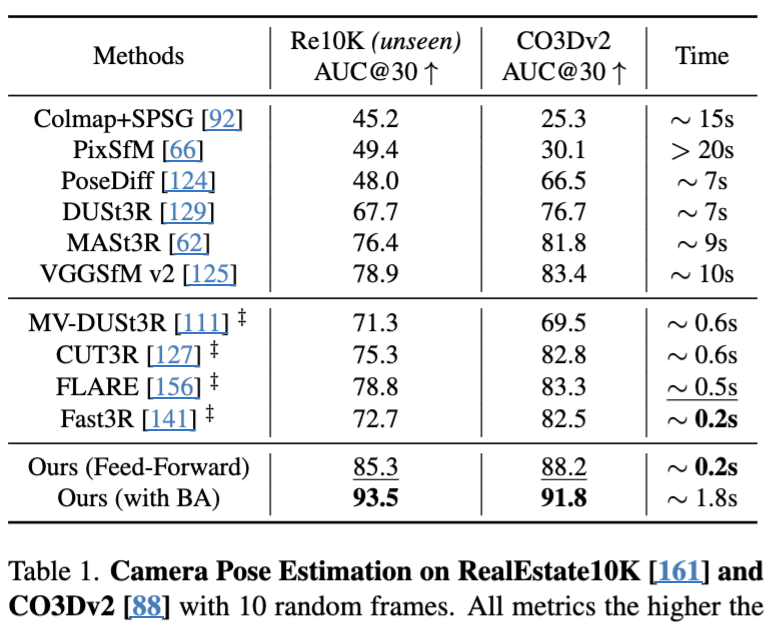
카메라 파라미터의 경우 Feed-forward 방식의 경우 가장 빠르면서도 가장 좋은 성능을 냈으며, BA와 같은 visual geometry optimization을 적용한 경우 속도는 느려졌지만 더 좋은 성능을 보였다.
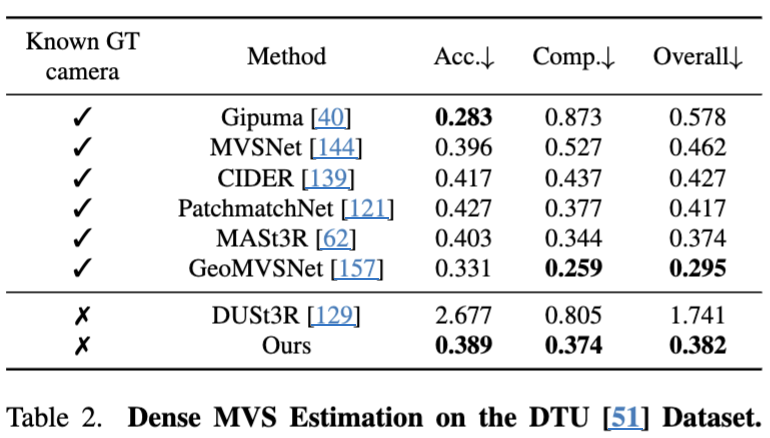
GT 카메라의 위치를 모르는 경우에서는 가장 좋은 성능을 보였고, 아는 경우에 비해서는 살짝 낮은 성능을 보였다.
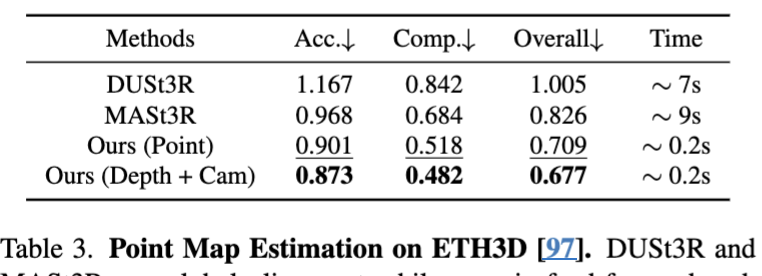
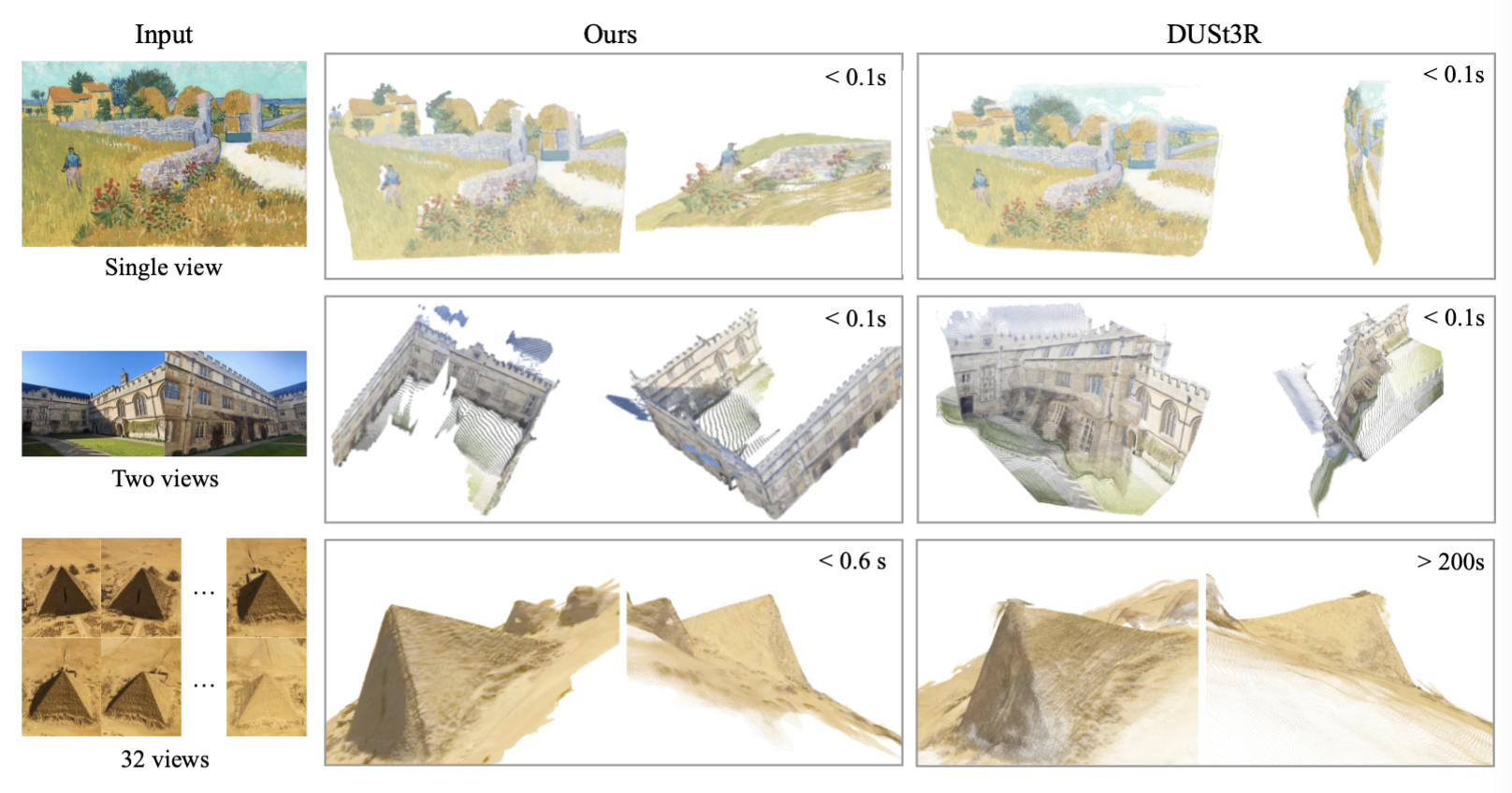

point map의 경우 좋은 성능을 보였고 figure를 보면 알 수 있듯이 높은 퀄리티와 다양한 도메인에서 할 수 있음을 알 수 있다.

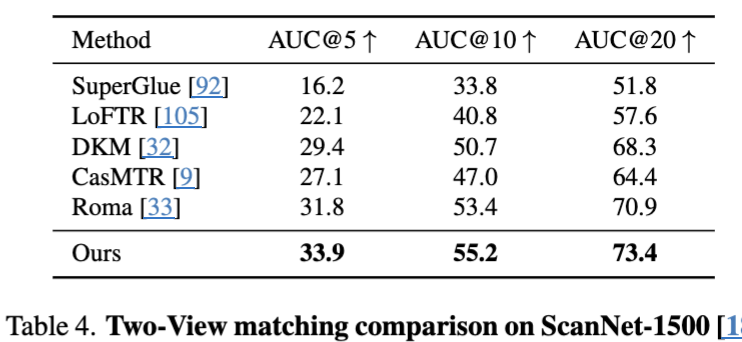
Tracking의 경우 VGGT가 2개의 view에 특화된 모델이 아님에도 가장 좋은 성능을 보였고, Tracking 예시 또한 위처럼 잘 동작하는 것을 볼 수 있다.
Novel View Synthesis

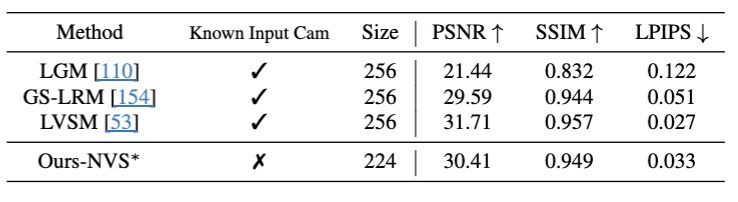
Feed forward Noverview Synthesis를 할 수 있는데 방식을 약간 수정해서 적용했고, LSVM 방식으로 비교할 경우 LSVM보다 살짝 낮은 성능을 보였지만 카메라 위치를 알 필요가 없다는 장점이 있다.
Ablation Study
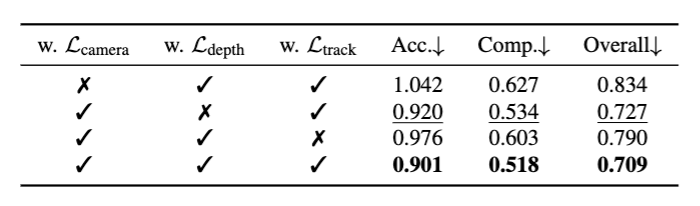
Loss 구성에 대한 Ablation study 결과로 3모듈을 넣었을 때 가장 좋은 성능을 보였다.

이 논문에서 제안한 Alternating Attention Module의 Ablation study 결과로 다른 Attention 대비 성능이 좋음을 알 수 있다.
Enjoy Reading This Article?
Here are some more articles you might like to read next: