Arxiv 2025
Bidipta Sarkar, Mattie Fellows, Juan Agustin Duque, Alistair Letcher, Antonio León Villares, Anya Sims, Dylan Cope, Jarek Liesen, Lukas Seier, Theo Wolf, Uljad Berdica, Alexander David Goldie, Aaron Courville, Karin Sevegnani, Shimon Whiteson, Jakob Nicolaus Foerster
20 Nov 2025
[paper]

preliminary

Low Rank Matrix Approximations

고차원의 파운데이션 모델을 파인튜닝할 때 gradient base 방식은 많은 메모리를 필요로 한다. 여기서 대표적인 파인튜닝 기법인 LoRA는 행렬곱 연산에서 low-rank approximations를 사용해 비용을 낮춘다. 모델에 있는 각 matrix $M_i \in \mathbb{R}^{m \times n}$ (모델에는 많은 M 있음)에 대해

\[M_i \approx M_i^0 + A_i B_i^\top\]

다음과 같이 $M_i^0$는 Frozen Pre-trained Weights로 모델이 원래 가지고 있던 지식이고 이 값은 수정하지 않아 메모리 절약의 핵심이 된다. $A_i B_i^\top$는 Trainable Adapter로서 모델에서 조금 순정된 값이 된다. 이때 A,B는 $A_i \in \mathbb{R}^{m \times r} , B_i \in \mathbb{R}^{n \times r}$로 $r \ll \min(m, n)$를 만족하여 매우 적은 파라미터만을 학습해도 되는 문제로 바뀌게 된다. 이때 학습해야하는 파라미터의 수가 mn에서 r(m+n)으로 바뀌게 되어 학습할 파라미터가 줄어들게 된다.

Gaussian Matrix Distribution and Matrix Norms

파라미터가 벡터가 아닌 행렬일 때, 랜덤한 노이즈를 생성하기 위한 식

\[\mathcal{N}(M,U,V) = \frac{1}{(2\pi)^{\frac{mn}{2}} \det(U)^{\frac{n}{2}} \det(V)^{\frac{m}{2}}} \exp \left( -\frac{1}{2} \operatorname{tr} \left( V^{-1}(X - M)^{\top} U^{-1}(X - M) \right) \right)\]

• X : 생성되는 Matrix
• M : 생성되는 Matrix의 평균
• U, V : 행, 열의 Covariance Matrix

이때 이걸 행렬로 생각하던, 길게 펴 벡터로 생각하던 수학적으로는 똑같다. $vec(X)$는 한줄로 핀 벡터인데, $\Sigma = V \otimes U$를 만족하는데, $\Sigma$가 covriance matrix가 된다.

\[\left\Vert M \right\Vert_F := \sqrt{\sum_{i,j} m_{i,j}^2},\]

그리고 행렬과 행렬 사이의 거리를 재거나 원점으로부터의 거리를 보기 위해 Frobenius Norm를 사용한다. 행렬 버전 피타고라스라고 생각하면 되는데, 행렬 안의 모든 숫자를 제곱해서 더하고 루트 씌운것이다.

Evolution strategies(ES)

ES는 시스템이 미분가능하지 않거나 노이즈가 많은 상황일때 사용할 수 있는 블랙박스 최적화 기법이다. 우리의 목표는 fitness 함수(해가 얼마나 좋은지 최적화하는 함수, 값을 극대화해야 함)를 극대화하는 $M^*$을 찾는 것이다. ($M^\star \in \underset{M \in \mathbb{R}^{m \times n}}{\text{arg max}} f(M)$)

\[J(\theta) = \mathbb{E}_{M \sim \pi(M|\theta)} [f(M)]\]

기존 gradient 방식은 M을 직접 수정하지만, ES는 $\theta$가 모델의 파라미터 모집단의 분포($\pi$)를 수정하여, 그 모델의 fitness를 극대화 시키는 쪽으로 $\theta$를 수정시킨다. 다시 말해 모델의 파라미터를 분포라고 가정하고, 그 분포를 fitness function이 극대화하는 쪽으로 분포를 이동시키는 것이다.

\[\nabla_\theta J(\theta) = \mathbb{E}_{M \sim \pi(M|\theta)} \left[ \nabla_M \log \pi(M|\theta) f(M) \right]\]

위 J를 미분하면 위와 같은 식이 나오게되고(증명은 생략)

\[\theta_{t+1} \leftarrow \theta_t + \alpha_t \nabla_\theta J(\theta_t)\]

이 gradient를 파라미터($\theta$)를 최적화 시키기 위해 SGD할 때 사용하게 된다. 이때 $\nabla_M \log \pi(M|\theta) f(M)$는 score function이라고도 불리며, fitness를 직접 미분해서 gradient를 얻는걸 막아준다.

Gaussian Matrix ES

우리가 찾고자하는 행렬 M의 경우 위에서와 같이 $\pi(M |\theta) = \mathcal{N}(\mu, I_m\sigma^2, I_n\sigma^2)$ 다음과 같은 분포에서 뽑아낸다고 가정할 수 있다. 이를 가우시안으로 하는 이유는 수학적으로 편할 뿐더러, 중심극한정리에 의해 낮은 랭크의 근사가 랭크가 커지면(표본이 늘어나면) 자연스럽게 가우시안 분포를 띄기 때문이다.

\[J(\mu) = \mathbb{E}_{E \sim P(E)} [f(M = \mu + \sigma E)].\] \[\nabla_{\mu} J(\mu) = - \frac{1}{\sigma} \mathbb{E}_{E \sim P(E)} [E \cdot f(M = \mu + \sigma E)]\]

따라서 위의 J 수식을 위와 같이 표기할 수 있고, $\mu^2$는 고정하고 $\theta = \mu$를 최적화한다. 여기서 $P(E)$ ~ $\mathcal{N}(0, I_m\sigma^2, I_n\sigma^2)$이고 natural gradient는 $\sigma^2\nabla_\theta J(\theta)$와 같다.

여기서 핵심은 ES와 NES(Natural ES)는 동치라는 것이다. 구체적으로는 NES는 파라미터 공간내에서 실제 gemotry를 고려하여 가장 효율적으로 확률 분포를 찾지만, 수학적으로 구해내기 어렵다. 하지만 우리가 $\mu^2$는 고정한다고 했으니 사실상 방향은 똑같은 상수배라 볼 수 있고 이는 이론적으로 똑같아진다. 따라서 더 계산하기 쉬운 ES를 통해 더 좋은 NES를 통해 계산이 가능해진다.

Related work

Evolutionary Algorithms

Evolutionary Algorithm은 backpropagation의 매력적인 대안이 되어왔다.Genetic Algorithms나 Symbolic Evolution와 같은 알고리즘이 나옴에도 불구하고, 최신 연구는 스케일을 키우는 방향으로 연구가 진행되었다.

해당 연구는 NES 방법론을 기반으로 가중치를 evolution시키는데 초점을 맞춘다. 특히 최근 연구에서 강화학습의 policy learning에서 NES를 적용한 연구에서 long horizon(긴 시간)에서 생기는 어려움을 해결하면서 중요성이 커졌다.

여기서 해당연구는 작은 네트워크를 넘어 기존 1440개의 population을 수십만개까지 키우는데 집중한다. ES는 긴 시간 동안의 시뮬레이팅 정책을 기록해야하기에 fitness function을 계산하는데 많은 비용이 든다. Persistent Evolution Strategies 연구에서 실시간으로 이를 계산하므로 인해 상당한 속도 향상을 보였고, 후속연구로 variance를 줄이는 연구가 진행되었지만, 저자는 이를 population 크기 자체를 키우는 문제와는 다른 문제로 보고 있다. (증명은 Appendix A.1 참고)

Evolution Strategies for LLMs

gradient backpropagation이 LLM training과 finetuning에서 많이 사용되긴하지만, ES의 변형을 도입하고자하는 시도들이 있었다. population 크기가 1과 유사한 ‘zeroth order optimization’는 효율적인 LLM finetuning 기법으로 사용되었고, 이에 확장으로 노이즈(perturbations)를 낮은 랭크의 부분공간으로 투영해서 속도를 개선하거나, LoRA 행렬에 직접 ES를 시도하기도 하였다.

여기서 finetuning이 아닌 pretrain을 하기 위해선 거대한 population의 크기가 필요하다는 것을 확인했고, zeroth order optimization이 pretrain에는 부적합함을 시사한다.

또한 LLM 추론 단계에서도 ES가 활용되는데, SFT(supervised fine-tuning)을 통해 LoRA 어댑터 훈련 후, CMA-ES로 훈련되는 singular value와 고정된 SVD의 bases(기저)로 분해하는 방식을 통해 추론 시간을 매우 줄이면서, 더 좋은 성능을 보이기도 하였다.

하지만 위 방법은 모두 업데이트당 수백개 정도의 unique perturbations를 사용하고, GPU 효율을 위해 각 perturbation당 수백번의 rollouts을 수집하는 방식을 취한다. 하지만 이 연구에서 제안하는 방식은 토큰 생성량은 줄어들지 않으면서 모든 생성 과정에서 다른 perturbations를 사용할 수 있게 되어, 업데이트당 population는 전보다 훨씬 커지게 된다.

• perturbations는 기존의 파라미터가 $\mu$ 일때, $M = \mu + \sigma E$에서 E를 의미.
• 롤아웃은 모델을 한번 실행해보는 것을 의미. 즉 똑같은 걸로 100번테스트가 아닌, 다른 100개로 한번씩 테스트해보는게 낫다는 것.
• population은 테스트해보는 모델의 갯수를 의미
• 정리하자면 population을 왕창 늘려서, 롤아웃은 한번만 하겠다

Methodology

EGGROLL 수도코드

입력 파라미터

• $r$ : perturbations matrix를 만들때 사용하는 rank의 크기
• $\alpha$ : learning rate
• $\sigma$ : 탐색을 위해 더해주는 노이즈 크기
• $T_{max}$ : 전체 학습 반복 횟수
• $N_{workers}$ : 병렬로 실행할 워커 수, population size

수도코드 설명

• 작은 무작위 행렬 A, B를 생성
• 두 행렬을 곱해서 row rank perturbations matrix E를 만듬
• Fitness Evaluation : 원래 모델($\mu$)에 노이즈($\sigma E_i$)를 더한 변종 모델을 만들고, 돌려보고(롤아웃) 점수($f_i$)를 매긴다.
• 각 worker끼리 계산한 점수($f_i$)를 공유하고, 새로운 공유된 시드 $\varsigma$를 통해 각 모델마다 노이즈를 생성($E_j$)
• (노이즈 방향 x 그 노이즈의 점수) 의 평균 만큼 모델을 이동시킴

Low Rank Evolution Strategies

가정 1 (Assumption 1) : $A$의 모든 원소 $a_{i,j}$와 $B$의 원소 $b_{i,j}$는 평균이 0이고 대칭적이며 절대 연속적인 분포 $p_0(\cdot)$를 따르는 연속적이고 독립적이며 동일한 분포(i.i.d.)의 확률 변수라고 가정합니다. 또한, 이 분포는 유한한 4차 모멘트와 분산 $0 < \sigma_0^2$(분산이 0이면 안된다, 즉 최소한의 무작위성을 가져야한다.)를 가집니다.

* Moment란

1차 모멘트 : 평균(중심), 2차 모멘트 : 표준편차(퍼진정도), 3차 모멘트 왜도(좌우 비대칭 정도), 4차 모멘트 : 첨도(kurtosis, 꼬리의 두께)

4차 모멘트가 유한하다 : 큰 값이 가끔 나올 수 있지만, 수학적으로 감당 불가능할 정도의 값은 나오지 않는다.(정리2에서 중심극한정리 쓰려고 필요)

row Rank 근사 $AB^T$를 Gaussian Matrix ES에 통합하킬 때, 열의 개수 r이 증가함에 따라 분산이 발산하는 것을 막기 위해 $\sqrt{r}$로 나누어준다. $AB^\top$ 계산은 r개의 외적 행렬을 더하는 과정으로 볼수 있고($AB^\top = \sum_{k=1}^{r} (\mathbf{a}_k \cdot \mathbf{b}_k^\top)$), r배 증가하는 분산을 막기 위해 $Var(CX) = C^2 Var(X)$성질을 이용해 $\frac{1}{\sqrt{r}}$만 곱해줌으로서 분산이 1이 되도록 하는 것이다.

여기서 $E = \frac{1}{\sqrt{r}}AB^\top$은 $\mathbb{R}^{m \times n}$ 공간의 부분집합 manifold $\mathbb{M}^r$에 맵핑된다. 이때 manifold의 부피가 0이 되므로 확률밀도함수에서 부피가 0이라 미분을 할 수가 없다. (E의 원소에 종속성이 있어 살짝 바꾸는게 불가능) 따라서 저자는 $Z = \frac{1}{\sqrt{r}}AB^\top + \epsilon$를 제안한다. 여기서 $\epsilon$은 independent decaying Gaussian elements인 $\epsilon_{i,j} \sim \mathcal{N}(0, \sigma_\epsilon^2/r)$이다. 이 Z는 모든 $\sigma_\epsilon > 0$에 대해 잘 정의된 밀도 함수 $p(Z)$를 가지게 되고, 임의로 $\sigma_\epsilon > 0$를 작게 만들어 $p(E)$와 $p(Z)$를 거의 같게 만들 수 있어, E 대신 Z를 사용할 수 있게 된다. 따라서 Gaussian Matrix ES의 식에서 E대신 Z를 넣어 low-rank ES objective와 Low-rank ES Gradient를 다음과 같이 쓸 수 있다.

\[J_{\text{LR}}(\mu) = \mathbb{E}_{Z \sim p(Z)} [f(M = \mu + \sigma Z)].\] \[\nabla_{\mu} J(\mu) = - \frac{1}{\sigma} \mathbb{E}_{E \sim P(E)} [E \cdot f(M = \mu + \sigma E)]\]

Score Function Approximation

$(A, B, \epsilon) \rightarrow Z = \frac{1}{\sqrt{r}}AB^\top + \epsilon$ 의 경우 non-invertible하므로, m=n=1과 같은 특수한 상황을 제외하면 p(Z)와 스코어 함수에 대한 진짜 해가 존재하지 않는다. 따라서 아래와 같이 스코어 함수에 대한 근사값을 사용한다. $\hat{S}(Z) \approx \nabla_Z \log p(Z)$

\[\hat{g}_{\text{LR}} = -\frac{1}{\sigma} \mathbb{E}_{Z \sim p(Z)} \left[ \hat{S}(Z) f(M = \mu + \sigma Z) \right]\]

여기서 스코어 함수의 근사를 얻기 위해 Gaussian approximate score function를 사용하는데 $r \rightarrow \infty$ 극한을 취함으로서 얻을 수 있다. $\epsilon$은 동등한 분포를 갖는 $r$개의 독립적인 가우시안 행렬들의 합으로, $AB^\top$도 독립적인 0-평균 벡터 외적의 합으로 분해될 수 있다.

\[\epsilon = \frac{1}{\sqrt{r}} \sum_{i=1}^{r} \epsilon_i,\] \[AB^\top = \sum_{i=1}^{r} a_i b_i^\top,\]

중심극한정리(Central Limit Theorem)에 의해 $p(Z)$는 분포상으로 가우시안 $\mathcal{N}(0, I_m \sigma_0^4, I_n \sigma_0^4)$에 수렴하게 되고, 이를 통해 가우시안 근사 스코어 함수를 얻을 수 있게 된다.

\[\hat{S}(Z) = - \frac{1}{\sigma_0^4} Z\]

EGGROLL UPDATE

여기서 $\hat{g}_{\text{LR}}$의 기대값을 $N_{workers}$로 Monte Carlo estimate로 근사한 값을 stochastic gradient ascent를 통해 파라미터 최적화를 진행한다.

각 worker는 $A_{i,t} \sim p(A_{i,t}), B_{i,t} \sim p(B_{i,t})$를 샘플링하고 row rank perturbations $E_{i,t} = \frac{1}{\sqrt{r}}A_{i,t}B_{i,t}^\top$를 형성하고, 행렬의 파라미터를 다음과 같은 수식을 통해 업데이트한다.

\[\mu_{t+1} = \mu_t + \frac{\alpha_t}{N_{\text{workers}}} \sum_{i=1}^{N_{\text{workers}}} E_{i,t} f(M = \mu_t + \sigma E_{i,t}).\]

이때 $\frac{1}{\sigma}$와 $\frac{1}{\sigma_0^4}$는 상수 이므로 $\alpha_t$에 흡수시키고, $E_{i,t}$는 rank가 r이지만, 행렬 업데이트는 $N_{workers}$의 합이므로, 파라미터 업데이트의 rank는 $\min(Nr, m, n)$가 되고, 이는 파라미터 업데이트가 row rank로 제한되지 않음을 시사한다. 다시 말해 학습과정에서는 gpu가 각각 low rank로 돌리지만, 학습에 쓰이는 업데이트는 full rank가 된다 -> 메모리는 적게 쓰면서 성능은 잃지 않을 수 있다.

Hardware-Efficient EGGROLL Implementation

EGGROLL이 표준 ES보다 효율적인 이유는 low-rank perturbations이 GPU상에서 대규모 population으로 병렬 시뮬레이션이 가능하기 때문이다. 단일 워커 하나를 예시로 들면

입력 $x_i \in \mathbb{R}^{d_{in}}$와 평균 파라미터 $\mu \in \mathbb{R}^{d_{out} \times d_{in}}$를 갖는 선형 레이어의 순전파 작업은, 일반행렬곱 $x\mu^T$로 이루어진다. 여기서 표준 ES를 $x_i(\mu + \sigma E_i)^T$와 같이 사용하게 되면 $\mu + \sigma E_i$의 모든 요소가 한번만 곱셈되어 arithmetic intensity가 낮아지며 GP가 효율적이게 쓰이지 못한다.

하지만 EGGROLL은 $x_i(\mu + \sigma E_i)^T = x_i\mu^T + \frac{\sigma}{\sqrt{r}} (x_i B_i)A_i^T$의 공식이 쓰이며 대부분의 연산이 일반 행렬곱에서 $x_i\mu^T$를 효율적으로 계산할때 사용된다. 이때 r=1 일경우 $x_i B_i$가 값싼 배치 벡터-벡터 내적이 되어 스칼라 배치를 얻을 수 있고, $A_i^T$에서 스칼라 벡터 곱으로 처리되며, 이러한 분해 방식이 vLLM과 같은 LoRA 추론의 핵심이 되며, EGGROLL이 LoRA와 동일한 속도를 달성한다.

그리고 가우시안 근사 스코어 함수의 핵심항인 $\sum_{i=1}^N E_i f_i$을 계산할 때 $E_i$($A_i B_i^T$)를 메모리에 materializing하지 않음으로서 업데이트 과정을 더 최적화한다. 즉 한번에 E를 만들어서 메모리에 올리는게 아니라, A의 각줄에 f를 곱하고, $B^T$를 한번에 곱해서 해결($(A \odot f)B^T$)할 수 있다.

Approximation Analysis

Gaussian score approximation가 True Gaussian ES matrix gradient에 얼마나 빠르게 수렴하는지 분석한다. 이를 위해 fitness function에 regularity assumption를 도입한다.

가정 2 (Assumption 2) : $f(M)$은 bounded라고 가정. 즉, $\sup_M|f(M)|<\infty$

진짜 full rank gaussian ES gradient가 $g_{True} := \nabla_{\mu} J(\mu)$ 일때, $\hat{g}_{LR}^r$에서 low rank update gaussian score 근사값 사이의 오차를 Frobenius norm(행렬 크기 구하는 가장 기본적인 방법)으로 보이는게 목표

정리 2 (Theorem 2) 가정 1과 2가 성립하고 $\sigma_0 = 1$로 설정할 때, 다음이 성립

\[\left\| \hat{g}^r_{\text{LR}} - g_{\text{True}} \right\|_F = \mathcal{O}\left( \frac{1}{r} \right)\]

이때 중심극한정리는 $\frac{1}{\sqrt{r}}$의 속도로 줄어드는데, EGGROLL은 $\frac{1}{r}$의 속도로 수렴하여 r이 아주 크지 않더라도 full-rank만큼의 속도를 낼 수 있다. 이는 가정1에서 symmetry 덕분이며, 이는 Edgeworth expansion라는 것을 이용한 덕분이다. 이는 확률분포를 ‘limiting Gaussian distribution + 3차 이상의 cumulants에 의해 제어되는 감쇄 항들의 합’으로 구성되어있으며 오차항은 3차 항, 4차 항 등이 계속 더해지는 방식이며, 이중 가장 큰 오차의 원인은 3차항(좌우로 찌그러진 정도)이며 $\frac{1}{\sqrt{r}}$ 속도로 수렴한다. 여기서 우리가 사용하는 분포(A,B 등)은 0을 기준으로 symmetric하기 때문에 홀수번째 항들이 전부 0이 되어 사라지게 된다. 그러면 그 다음 큰 오차를 발생하는 원인은 4차항인데, 4차 항이 $\frac{1}{r}$ 속도로 줄어 들게 되어 전체 오차 또한 $\frac{1}{r}$의 속도로 줄어들게 된다.

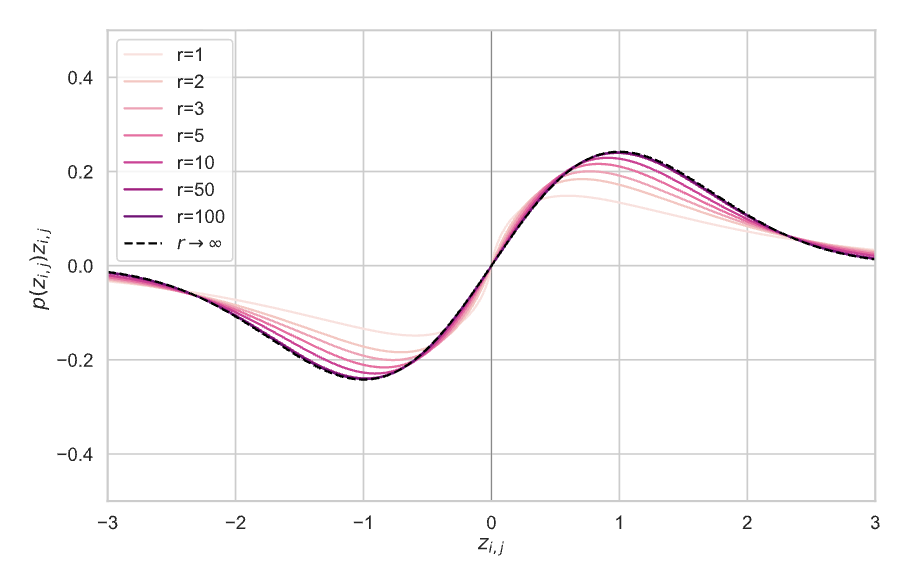
이 이미지를 보면 검정 선이 $r \rightarrow \infty$ 일때, 즉 완벽한 가우시안 분포(full rank)이데, 분홍선이 EGGROLL이 사용하는 저랭크 근사 분포이다. 그 결과 r=1일때도 모양이 비슷하지만 r이 증가함에 따라 검정색과 점점 구분이 안되는 모습을 볼 수 있었다.

Experiments

Pure Integer Pretraining of an RNN Language M

EGGROLL은 그라디언트에 의존하지 않으므로 inference에 효율적인 아키텍처를 구성할 수 있었다. 이때 H100에서 빠른 int8을 데이터 타입으로 채택했으며, Backpropagation Through Time이 필요 없기 때문에 minGRU를 변형해서 모델을 구성한다. 그리고 int8 데이터 자체가 비선형성을 지니므로 모든 activation function을 제거했다고 한다.

이렇게 만들어진 언어모델을 Evolved Generative GRU(EGG)라 부르며 EGGROLL에 친환적인 아키텍처라 한다. 이는 트랜스포머 디코더 모델과 비슷하지만 L2 정규화 대신 L1 정규화를, self attention 대신 GRU를, 그리고 모든 연산을 정수로 수행한다는 특징이 있다.

이때 최대 population 크기는 $2^{18} = 262,144$로 기존보다 100배 큰 규모이며, 1개의 GPU로만 학습이 가능하다고 한다.

Reinforcement Learning Tasks

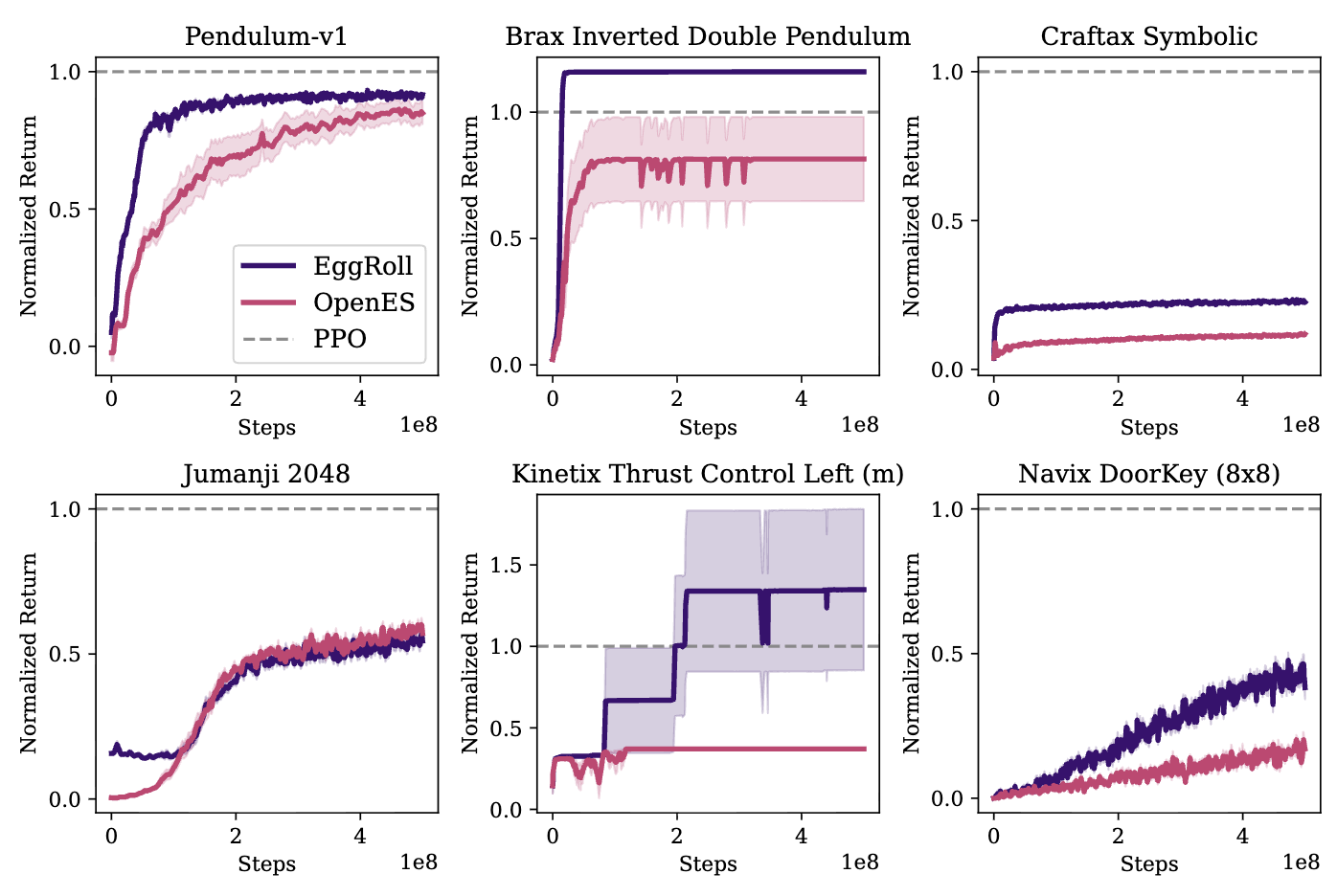
EGGROLL의 성능을 OpenES와 비교한다. 즉 Full-rank인 OpenES 대비 row-rank 근사의 성능이 떨어지는게 아닌지 확인하는 것이다. 그 결과 16개의 게임에서 EGGROLL이 14번 승리 혹은 무승부를 하였다. 따라서 EGGROLL이 단순히 메모리만 줄이는게 아니라 학습 효율성도 좋다는 것을 알 수 있다.

LLM Fine-tuning for Reasoning Tasks

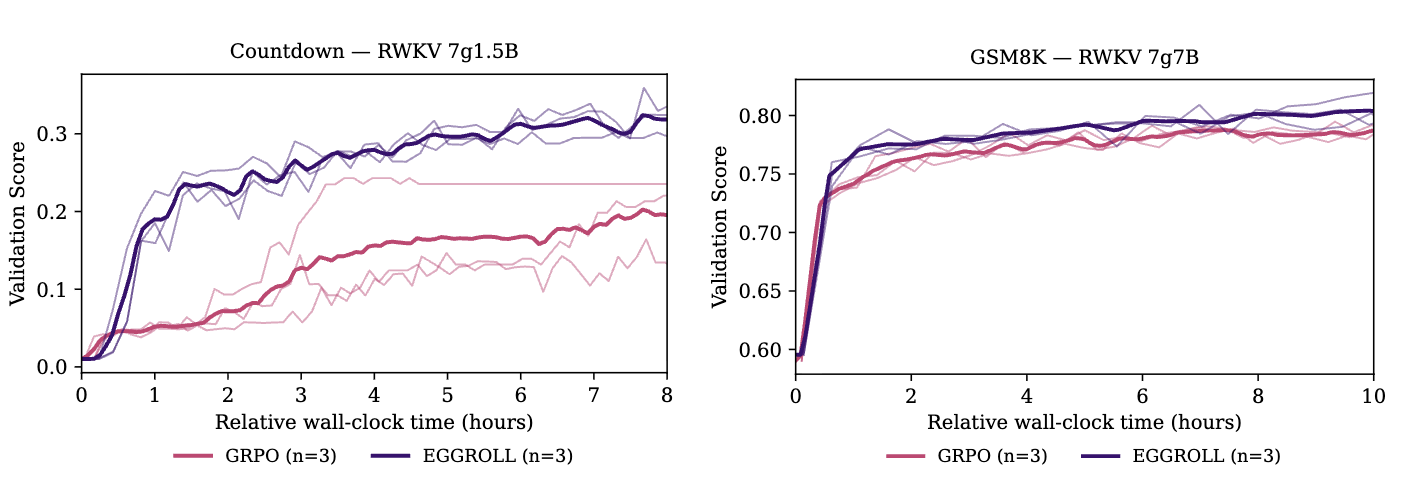
여기선 두가지 추론과제 Countdown과 GSM8K에서 모델 RWKV-7를 파인튜닝하기 위해 EGGROLL을 사용한 케이스이다. RWKV은 recurrent 모델로 트랜스포머 대비 병렬화에 유리하며 KV 캐시에 사용할 메모리를 population member를 평가할 때 쓸 수 있어 효율적이다.(트랜스포머 대신 RNN 계열 선택이유) 위 사진을 보면 두 과제에서 모두 동일 하드웨어, 소요시간 일때 더 좋은 성능을 보이는 것을 알 수 있다.