Series

Diffusion

Diffusion 모델에 대한 내용 정리

VAE (Variational Auto-Encoder)
DDPM(Denoising Diffusion Probabilistic Models) 설명 현재 글

2편 중 2편

Introduction

Diffusion 모델은 현재 Computer Vision에서 생성분야에서 가장 많이 쓰이는 모델이라고 봐도 과언이 아니다. 그 중 Diffusion 모델의 폭발적인 성장의 시작점이 되는 2020년의 DDPM을 중심으로 알아보려한다.

Methodology

놀랍게도 Diffusion 모델은 2020년 DDPM에서 처음 제안된 모델이 아니다. Diffusion 모델은 2015년에 Deep Unsupervised Learning using Nonequilibrium Thermodynamics 논문에서 처음 제안 되었지만, 당시에 노이즈 예측방식이 정립되지 않고 낮은 컴퓨팅 파워과 당시 GAN의 발달로 인해 크게 주목받지 못했다.

Forward process q & Reverse process p

Noise를 추가하는 프로세스 q

\[\quad q(\mathbf{x}_t | \mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I})\]

이때 노이즈를 추가하는 forward process는 학습을 하지 않으며, 가우시안 분포를 따르는 노이즈를 조금씩 추가한다. 이때 해당 process를 diffusion process 라고도 한다. 이때 해당 프로세스는 별도의 학습을 통해 진행되는게 아니라 t가 Variance Schedule $\beta_t$가 0.0001 ~ 0.02로 조금씩 증가하게 된다. 따라서 t가 커지게 되면 평균은 이전 평균보다 살짝 작은 값, 분산은 조금씩 커지게 되며, 최종적으로는 평균이 0이 되며 완벽한 랜덤 가우시안 분포($N(x_T;0,I)$)가 될 것이다. 다르게 말하면 이전(t-1)상태보다 $\beta$만큼 다른 픽셀을, $\sqrt{1-\beta}$ 만큼 이전 픽셀을 선택하며, 점점 노이즈가 비율이 늘어나고 있다고 볼 수 있다.

\[q(\mathbf{x}_{1:T} | \mathbf{x}_0) := \prod_{t=1}^{T} q(\mathbf{x}_t | \mathbf{x}_{t-1})\]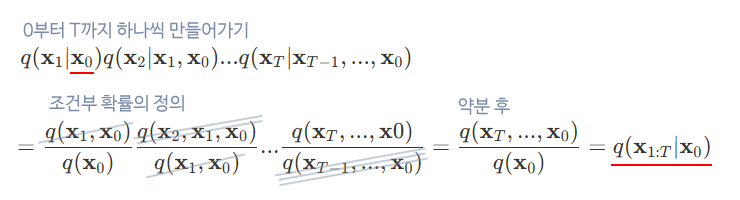

다음 식은 Fowward process를 조건부 결합분포(joint distribution)으로 나타낸 것이다. 이는 마르코프 체인가 현재 상태가 오직 바로 직전 상태에만 의존하고, 그 이전 상태들과는 독립인 원리를 이용해 식을 다음과 같이 변형 시킨 것이다.

\[q(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t}\mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I})\]

foward process는 학습되는 프로세스가 아니다. VAE에서 사용했던 reparameterization trick를 적용하여 $x_0$에서 특정 시점 t에서 노이즈가 추가된 이미지 $x_t$를 다음 공식을 통해 바로 얻어 낼 수 있다. 증명은 아래 이미지와 같다.

Noise를 걷어내는 프로세스 p

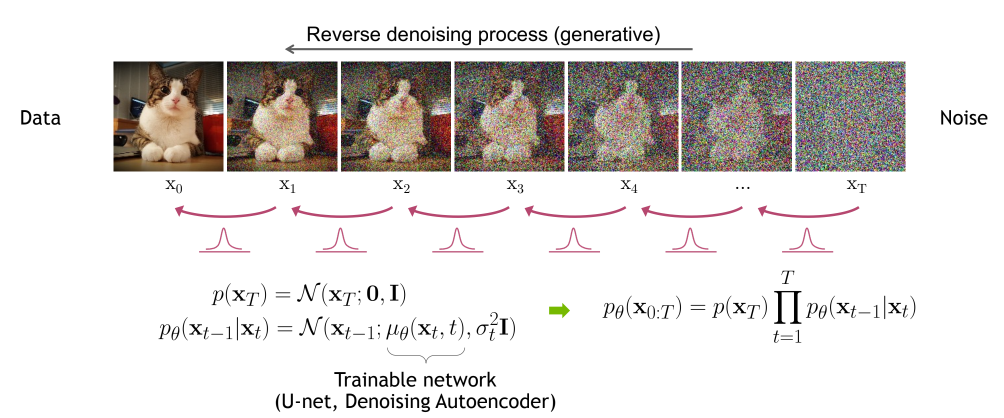
\[\quad p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) := \mathcal{N}(\mathbf{x}_{t-1}; \mu_{\theta}(\mathbf{x}_t, t), \Sigma_{\theta}(\mathbf{x}_t, t))\]

여기서 reverse process는 $p_\theta$라는 표현을 통해서 해당 단계에서 딥러닝을 한다는 것을 알 수 있고, forward공식과 비슷하게 공식이 생긴 것을 알 수 있다. 여기서 t번째 이미지에서 t-1번째 이미지를 만들기 위한 분포는 $\quad p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 다음과 같이 쓸 수 있고, 해당 분포의 $\mu_{\theta}$,$\Sigma_{\theta}$는 reverse process의 학습되는 평균과 표준편차임을 알 수 있다.

\[p_{\theta}(\mathbf{x}_{0:T}) := p(\mathbf{x}_T) \prod_{t=1}^{T} p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t),\]

reverse process 또한 마르코프 체인으로 표현할 수 있으며, 살짝 식이 다른 모습을 볼 수 있다.

Loss Function

딥러닝 학습을 통해 reverse process의 분포를 학습한다고 했으니, loss function을 정의해야한다. 이때 diffusion 모델이 실제 데이터의 분포를 잘 익혀야 하므로, $p_\theta(x_0)$의 likelihood를 최대화하면 될 것이다. 따라서 Negative Log Likelihood를 구하면 된다.

$p_\theta(x_0)$의 Negative Log Likelihood로부터 ELBO를 유도하는 과정이다. 여기서 $q(\mathbf{x}_0)$는 실제 데이터의 분포로 볼 수 있고, q에 대해 평균을 구한다는건 모든 데이터셋에 대한 평균을 구하는것을 의미한다. 여기서 Negative Log Likelihood를 최소화하는 문제에서 ELBO 최대화 시키는 문제로 바뀌게 된다.

위에서 구한 $\mathbb{E}_q\left[-\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\right]$에서 위에 정의된 마르코프 체인 버전으로 교체하고 식을 잘 전개하면 다음과 같은 loss 식을 얻을 수 있다.

\[\mathbb{E}[-\log p_\theta(\mathbf{x}_0)] \leq \mathbb{E}_q\left[-\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\right] = \mathbb{E}_q\left[-\log p(\mathbf{x}_T) - \sum_{t \geq 1} \log \frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\right] =: L \quad (3)\]

다시 한번 요약하자면 다음과 같이 작성할 수 있고

\[\mathbb{E}_q \left[ \underbrace{D_{KL} (q (\mathbf{x}_T | \mathbf{x}_0) \parallel p (\mathbf{x}_T))}_{L_T} + \underbrace{\sum_{t>1} D_{KL} (q (\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t))}_{L_{t-1}} - \underbrace{\log p_\theta (\mathbf{x}_0 | \mathbf{x}_1)}_{L_0} \right]\]

DDPM 논문에 명시된 Loss는 다음과 같이 3개의 항으로 해석하게 된다.

$L_T$ : $q (\mathbf{x}_T | \mathbf{x}_0)$와 $p (\mathbf{x}_T)$의 KL Divergence, 즉 Forward Process가 얼마나 가우시안 노이즈로 잘 바꾸냐를 의미. 하지만 DDPM은 Forward Process가 학습하는 과정이 아니므로 상수, 즉 생략 가능
$L_{T-1}$(이게 가장 중요!) : $q (\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)$와 $p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t)$의 KL Divergence의 합, Reverse Process가 이전 스텝의 이미지를 얼마나 잘 복원해내는지를 의미
$L_T$ : $x_1$에서 $x_0$를 얼마나 잘 복원해내는지로 보통 T가 크므로 굉장히 작은값으로 생략 가능

따라서 $L_{T-1}$를 구하기 위해 $q (\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)$와 $p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t)$를 구해야한다.

$q (\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)$의 평균과 분산

맨 아래서 나온 수식에서 가우시안 분포의 지수항에 있는 평균과 분산을 뽑아낼 수 있다. 따라서 $q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I})$ 일때 평균과 분산을 다음과 같이 쓸 수 있다.

\[\tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\] \[\tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t\]

여기서 평균을 다음과 같이 한번 더 전개하여 다음과 같은 노이즈가 포함된 식으로 쓸 수 있다.

$p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_t)$의 평균과 분산

$p_\theta$는 위에서 말했듯 학습을통해 얻게되는 분포이다. 여기서 해당 분포(모델)이 해야할 것은 $\mu_\theta$이 $\tilde{\mu}t$와 동일하게 만들어지면 되는 것이다. 따라서 $\epsilon$(실제 노이즈)을 $\epsilon\theta$(모델이 예측한 노이즈)로 바꾸기만 하면 된다. 따라서 해당 분포에서의 평균은 노이즈만 바뀐

\[\mu_\theta(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(\mathbf{x}_t, t) \right)\]

가 된다.

$L_{t-1}$ 및 Final Loss

최종적으로 위의 두 분포의 평균을 알고 있으니 두 분포 사이의 KL-divergence를 구할 수 있다. 이때 두 분포는 가우시안 분포이기에 아래와 같이 KL-divergence를 표기할 수 있다.

\[D_{KL}(p\|q) = \log \frac{\sigma_2}{\sigma_1} + \frac{\sigma_1^2 + (\mu_1 - \mu_2)^2}{2\sigma_2^2} - \frac{1}{2}\]

위 식에서 DDPM은 표준편차(분산)는 모두 상수이므로 식에서 다 제거하면 결국
$(\mu_1 - \mu_2)^2$만 남게되고 이를 대입해서 계산하면 다음과 같다.

다시한번 정리하자면 최종 정리된 Loss는 다음과 같이 정의된다.

\[\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \frac{1}{2\sigma_t^2} \left\| \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t(\mathbf{x}_0, \boldsymbol{\epsilon}) - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon} \right) - \boldsymbol{\mu}_{\theta}(\mathbf{x}_t(\mathbf{x}_0, \boldsymbol{\epsilon}), t) \right\|^2 \right]\]

해당 수식은 결국 정답 노이즈($\epsilon$)와 모델이 예측한 노이즈($\epsilon_\theta$)의 차이(MSE)를 줄이는 수식이 된다.