생성 ? 확률 ?

distribution of true p(x) is intractable sampling is also intractable tractable q(x) is …ed by neural net to approximate true p(x)

생성 모델을 공부하면 다음과 같은 문장을 맞닥드릴수 있다. 우리가 어떤 이미지를 생성하기 위해선 특정 분포에서 샘플링을 통해 진행이된다. 예를들어 위는 전체적으로 파란계열의 이미지를 얻기 위해선 RGB에서 B가 $\mathcal{U}(0.9, 1)$ 분포에서 샘플링하면 될것이고, 위가 어둡고 아래가 밝은 이미지를 얻으려면 위는 $\mathcal{U}(0, 0.5)$, 아래는 $\mathcal{U}(0.5, 1)$인 분포에서 샘플링하면 될것이다.

그렇다면 복잡한 이미지(ex. 고양이)를 생성하려면 어떻게 하면될까? 당연하게도 고양이를 생성하는 분포에서 샘플링하면 될 것이다. 하지만 실제 고양이를 생성하는 분포를 찾는 것은 불가능에 가까울 것이다. 따라서 우리는 고양이를 만드는 분포에 근사한 분포를 얻어낼 것이다. 그리고 이는 많은 고양이 사진, 즉 데이터로 부터 그 분포를 얻어내는 것이다.

인코더 (Encoder)

인코딩 : 데이터 공간을 압축해서 정보를 표현하는 방식. 이때 원래의 데이터로 되돌아 갈 수 있어야 의미가 있음.

인코더 : 인코딩을 수행하는 알고리즘

인코더는 두개의 특징이 존재한다.

특징 1. 가정이 있어야한다. 인코더는 더 적은 데이터 공간에 표현 가능하므로 데이터에 가정이 존재해야한다. 예를들어 이미지의 경우 어떤 부분엔 공통된 패턴이 나온다거나, 모서리는 RGB이 어둡다와 같은 가정이 필연적으로 필요하다.

특징 2. 인코더 공식은 여러개일 수 있다. 말 그대로다. 데이터를 더 적은 데이터 공간에 압축해서 표현할 수만 있다면, 표현은 굉장히 다양할 수 있다는 뜻이다.

오토인코더 (Auto-Encoder)

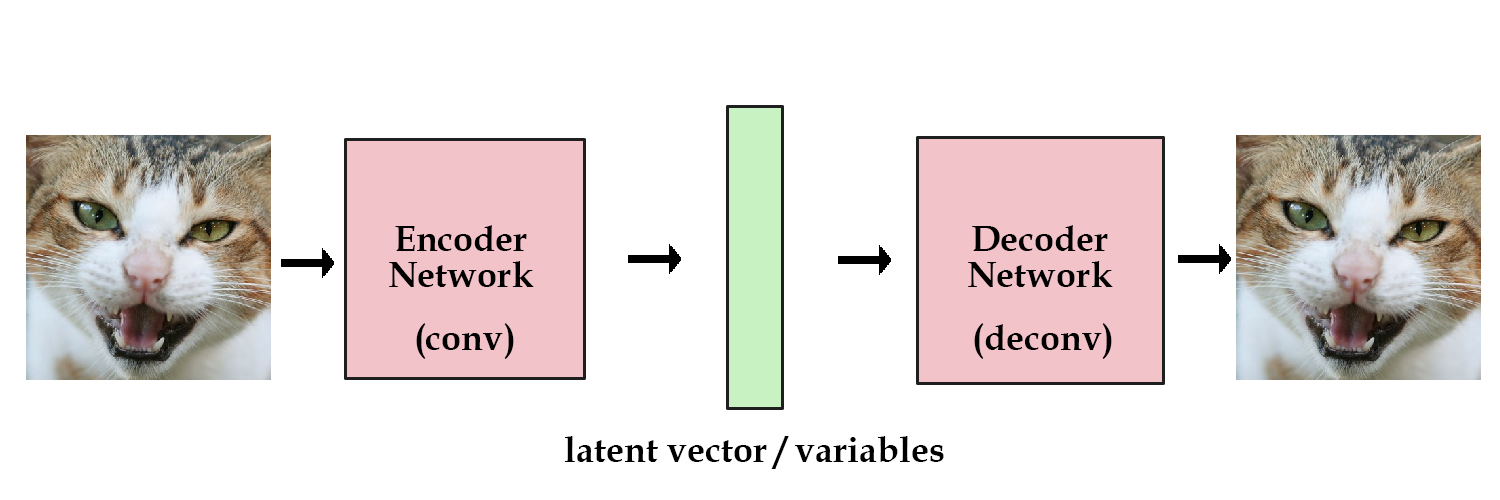
그래서 위에서 인코더는 데이터를 더 적은 데이터 공간으로 압축해주는 알고리즘이라 했고, 디코더는 이 압축된 데이터를 원본데이터로 되돌려주는 알고리즘이다.

이 인코더와 디코더를 직접 설계해서 찾을 수 있지만 그렇게 될 경우 2가지 문제점이 생긴다.

1. 매번 어떤 데이터의 특징을 찾는 것은 쉬운일이 아니다. 32x32 픽셀의 이미지는 3072차원의 데이터에서 패턴을 찾는건 매우 어려울 뿐더러, 이걸 찾는다 하더라도 매번 이 일을 할 순 없다.
2. 인코딩과 디코딩에서 패턴을 찾을때, 찾은 패턴이 실제 데이터와 오차가 있다면 데이터를 정확히 인코딩하고 복원할 수 없다.

따라서 여기서 패턴을 찾는것(공식을 만드는것)을 자동으로 해준다 하여 오토인코더가 등장한다. 입력한 데이터를 더 작은 차원으로 인코딩 시키고, 다시 아까 입력한 데이터와 동일한 데이터로 복원시키게 만든 모델을 오토인코더라 한다.

자 여기서 처음에 생성모델의 원리에 대해 다시한번 되돌아보자. 생성모델은 특정 분포에서 샘플링하여 데이터를 얻어내는 것이다. 그런데 문제는 오토인코더는 자동으로 데이터를 인코딩 시키는 것이고, 어디에 인코딩 시킬지는 모른다. 즉 오토인코더가 인코딩 시킨 분포 내에서 샘플링 하여 데이터를 만들어 낼 수 없기 때문에 오토인코더로 우리가 생각하는 생성모델을 만드는 것은 불가능하다.

VAE (Variational Auto-Encoder)

그래서 나온것이 VAE이다. 오토인코더는 인코딩된 데이터가 uniform분포나, 0 근처의 가우시안 분포로 모인다는 보장이 없다.

따라서 가장 쉽게 loss를 설계할때 loss = 인코딩 제곱평균 (0으로 몰기 위해) + (인코딩 - 인코딩의 평균) + 복원 loss($(x-\hat{x})^2$, 모든 z가 0에 가까워져 복원 안되는 것을 막기 위해)으로 하여 오토 인코더를 학습시키고, 입력데이터를 가우시안 분포에서 뽑아서 인코더는 건너 뛰고 아까 학습시킨 오토인코더의 디코더 부분에 넣으면 잘 나오는 것도 있지만 뭉개지는 케이스가 발생한다.

이는 생성(샘플링)은 확률적으로 뽑는 과정인데, 학습과정에서 확률적으로 무엇을 뽑는과정이 들어가지 않았다. 즉 학습할때 넣었던 데이터에 대해서만 잘 샘플링되는 것이다. 다시말해 오토인코더만으로 얻는 잠재공간은 원래의 이미지로 복구나 노이즈 제거 등에는 용이하지만, 샘플링을 통해 새로운 데이터를 생성하는데에는 한계가 있다.

그래서 VAE는 어떻게 하는거냐 싶을 수 있지만, 복잡하지 않게 구현적인 관점에서 보면 인코딩에 노이즈를 섞어서 디코더에 넣어주는 방식으로 구현된다. 그러면 학습과정 내에서 입력 데이터에 대해서만 학습하는게 아닌 인코딩 숫자 근처의 숫자들에 대해서도 본인이 나오게 학습이 진행된다. 쉽게 말해 조금 틀리더라도 복원해 낼 수 있게하는 기술이다. 즉 오토인코더와 VAE는 비슷하게 생겼지만 두 모델의 목적은 완전히 다른 것이다.

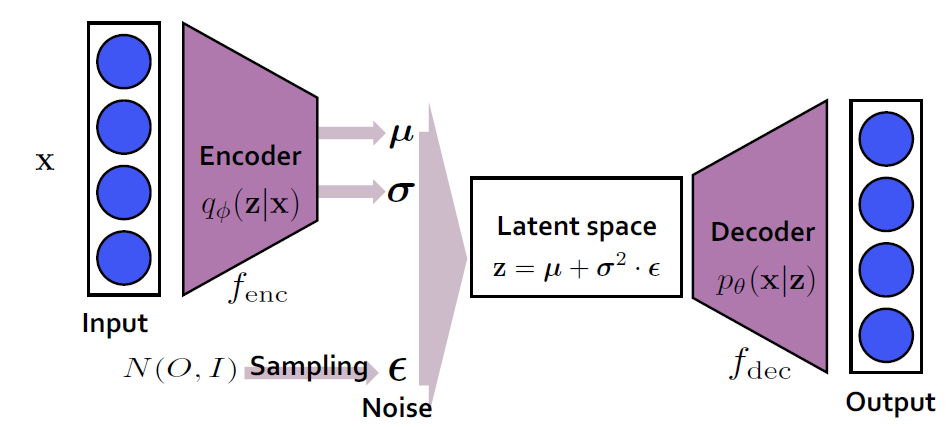
다음 이미지는 전체적인 VAE의 구조를 나타낸다. 위에선 간단히 말했지만 오토인코더에선 이미지를 바로 latent space로 축소되는 것과 다르게, 인코더의 출력으로 평균과 표준편차로 output으로 낸다. 그리고 정규분포에서 샘플링한 $\epsilon$과 평균 표준편차를 조합하여 z를 만들어서 이를 디코딩하게 되는게 원리이다. 여기서 살짝의 이해를 위해 틀리게 설명한 부분이 있지만 이게 전반적인 VAE의 설명이다. 이제 VAE가 구체적으로 뭔지 자세히 알아보자.

VAE 자세히 보기

Preliminaries

Entrophy

정보이론에서 엔트로피는 ‘정보를 표현하는데 필요한 최소한의 자원(비트)’을 의미한다. 다시말해 어떤 상태를 완벽하게 알기 위한 최소한의 질문 수로도 생각할 수 있다.

이때 엔트로피가 높은 케이스 = 확률이 균등할 때 = 최대 불확실성이다. 왜냐하면 예로 A,B,C,D가 나올 확률이 모두 25%라면 이를 인코딩할 때 모두에게 2비트씩 줘야하므로 $(0.25 \times 2) + (0.25 \times 2) + (0.25 \times 2) + (0.25 \times 2) = 2$로 엔트로피는 2비트이다.

반대로 이때 엔트로피가 낮은 케이스 = 확률이 쏠려 있을 때 = 낮은 불확실성이다. 다시 예를 들면 A(50%), B(12.5%), C(12.5%), D(25%)라 하면 자주 나오는 케이스에게 낮은 비트를 할당할 수 있게되고, 이 경우 $(0.5 \times 1) + (0.25 \times 2) + (0.125 \times 3) + (0.125 \times 3) = \textbf{1.75 비트}$ 더 낮은 비트로도 표현이 가능해진다.

다시 말해 데이터의 패턴이 명확할 수록 더 적은 질문(비트)로 데이터를 표현할 수 있게 된다는 것이다.

\[CE = \sum_{x \in \chi} (-P(x) \log(Q(x)))\]

그러면 딥러닝 분류문제에서 loss로 많이 사용되는 크로스 앤트로피는 무엇일까. 위 식에서 P(x)는 실제값, Q(x)는 모델이 예측값일때 크로스 앤트로피를 일반화한 식이다. 여기서 크로스 앤트로피는 우리의 모델이 정답(데이터)를 맞추기 위해 필요한 총 비용이라고 보면 된다. 이때 실제 데이터의 앤트로피가 있을텐데, 그 앤트로피와 해당 모델이 그 데이터를 해석하기 위해 더 많은 비용을 지불했을 것이다.(모델이 완벽하지 않을것이므로) 이때 실제 데이터의 앤트로피와 총 지불한 앤트로피의 차이가 KL-divergence라 부른다.

\[\underbrace{H(P, Q)}_{\text{크로스 엔트로피}} = \underbrace{H(P)}_{\text{엔트로피}} + \underbrace{D_{KL}(P || Q)}_{\text{KL Divergence}}\]

KL-divergence

\[D_{KL}(P || Q) = \sum_{x} P(x) \log \left( \frac{P(x)}{Q(x)} \right)\]

실제로 KL-divergence는 두 확률분포 P,Q 사이의 비율에 대한 로그 기대값이다. 직관적으로 보면 $P$ 대신 $Q$를 썼을 때 발생하는 정보량의 손실이라고 볼 수 있다.

\[= - \sum_{x \in \mathcal{X}} P(x) \log_b Q(x) + \sum_{x \in \mathcal{X}} P(x) \log_b P(x)\] \[\Rightarrow - E_P [\log_b Q(x)] + E_P [\log_b P(x)]\] \[\Rightarrow H_P(Q) - H(P)\]

이를 전개하면 P관점에서 본 Q의 크로스 엔트로피에서 P의 트로피를 뺀 것을 의미한다.

\[D_{KL}(P || Q) = \underbrace{H(P, Q)}_{\text{Cross Entropy}} - \underbrace{H(P)}_{\text{Entropy}}\] \[D_{KL}(P || Q) \neq D_{KL}(Q || P)\]

즉 다시 말해 위 수식은 P가 데이터 분포가 되고 Q가 모델이 되는 것이다. 따라서 순서가 영향을 미치며 바뀌면 의미가 달라진다.

Loss Function

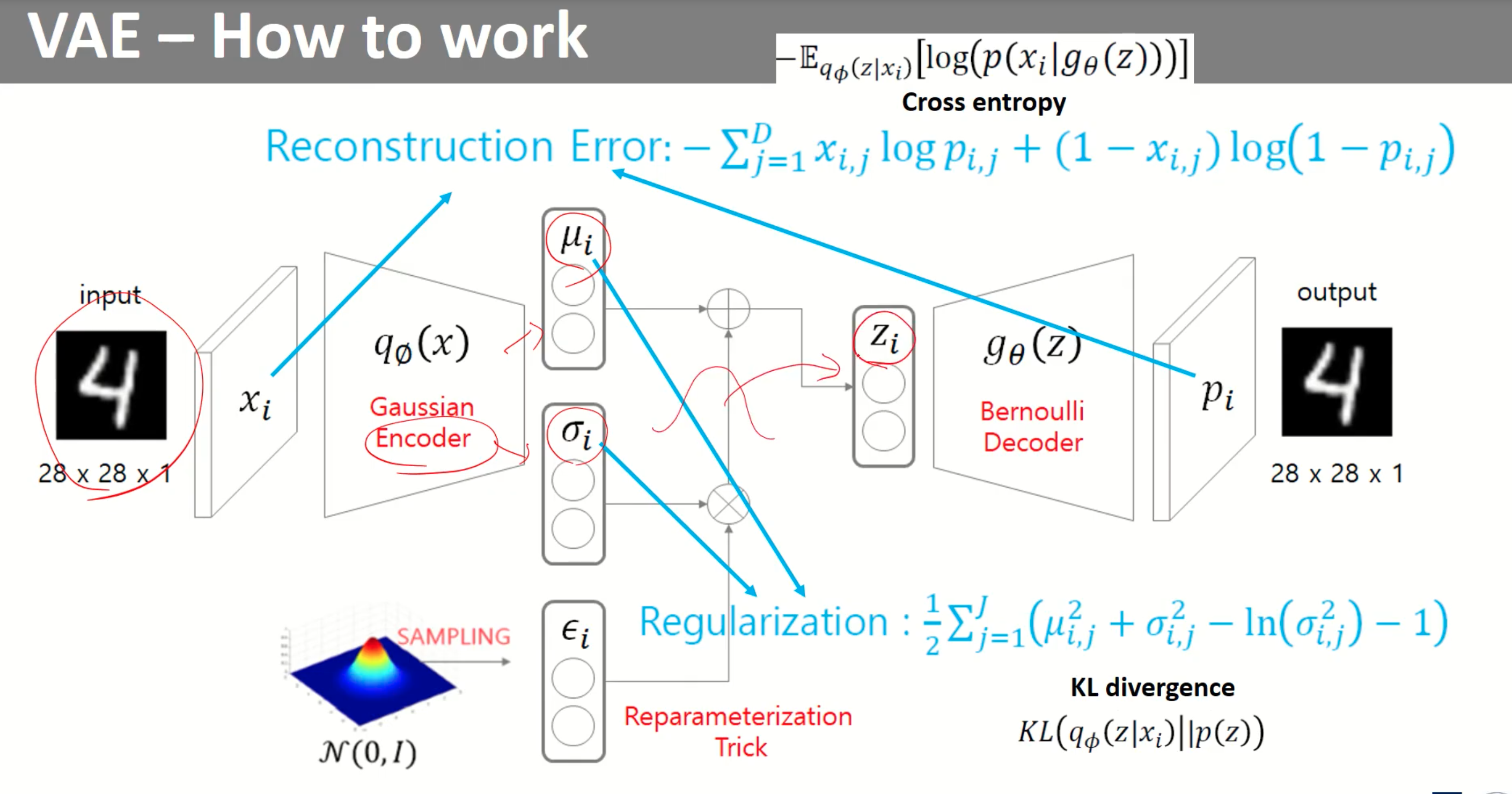
VAE는 2개의 Loss function이 존재한다. 여기서 VAE는 분포가 가우시안, 베르누이 분포 둘 다 가능한데 베르누이로 가정하고 loss function을 작성했다고한다. 먼저 Reconstruction Error는 오토인코더와 마찬가지로 입력값과 출력값 사이를 줄이기 위해 존재하며, Regulariztion Loss의 경우 VAE인코더는 가우시안의 평균과 표준편차를 출력으로 내야하는데, 이렇게 만들기 위해 KL-divergence를 통해 가우시안 분포의 형태로 만들어준다고 생각하면 된다.

어떻게하면 Generative Model의 파라미터 $\theta$를 최적화 할 수 있을까? Maximize Likelihood을 통해 진행된다. 따라서 $p_\theta(x)$를 구해내면 된다.

기호 정리

• $\theta$ : 우리 모델의 파라미터
• $\theta^*$ : 실제 데이터를 완벽하게 표현할 수 있는 이상적인 파라미터
• $p_{\theta^*}(z)$ (True Prior) : 원래의 잠재공간, 정규분포로 가정
• $p_{\theta^*}(x|z)$ (True Conditional) : z가 주어졌을때 데이터를 복구해낼 수 있는 분포, 즉 완벽한 디코더
• $p_\theta(x|z)$ : Conditional Likelihood (조건부 우도), latent variable이 z일때 x(데이터)가 나올 확률 -> 디코더 그 자체

\[p_\theta(x) = \int p_\theta(z)p_\theta(x|z)dz\]

우리는 $p_\theta(x)$를 구하기 위한 식이다. 여기서 $p_\theta(z)$는 정규분포라 가정하고, 그런데 위의 식에서 총 2가지 문제가 발생한다.

문제점 1: Evidence(\(p_\theta(x)\))를 구할 수 없다.

$p_\theta(x)$를 구하기 위해선 모든 latent variable z에 대한 적분값을 구해야한다. 이 모든 latent variable을 고려하면서 계산하는 것은 계산 불가능(Intractable)하다.

문제점 2: True Posterior($p_\theta(x|z)$)도 구할 수 없다.

위에서 p(x)를 구하는게 불가능하다 했으니 데이터($x$)를 보고 잠재 변수($z$)를 유추하는 진짜 확률 분포(Posterior)라도 구해보고 싶다.

\[p_\theta(z|x) = \frac{p_\theta(x|z)p_\theta(z)}{p_\theta(x)}\]

베이즈 정리에 의해서 다음과 같은 수식을 통해 $p_\theta(x|z)$를 얻을 수 있으나, $p_\theta(x)$를 구하는 것이 불가능하다고 문제점 1에서 말했으므로, 이또한 구하는게 불가능하다.

결론 : 통계적으로 완벽한 $z$를 역추적하는 것은 불가능. $p_\theta(z|x)$를 직접 계산하는 것은 불가능하기 때문에 이에 근사하는 $q_\phi(z|x)$를 도입하자. (참고 : 이 역할을 하는 q가 인코더!)

$p_\theta(x|z)$를 구하기 위한 수식은 다음과 같다.

첫번째 줄

$p_\theta(x|z)$에 그냥 로그를 씌운거고, z가 $q_\phi(z|x)$ 다음과 같은 분포를 따를때의 기대값과 같다. 그 이유는 z의 분포와 상관 없이 $\log p_\theta(x^{(i)})$는 상수값이므로, q를 등장시키기 위해서 넣었다고 생각하면 된다.

두번째 줄

$p_\theta(x^{(i)})$를 베이즈 정리를 이용해서 식을 변환해준다.

세번째 줄

어차피 약분하면 1이므로, 분모 분자에 $q_\phi(z|x)$을 곱해준다. 그 이유는KL Divergence 모양$\log \frac{q}{p}$으로 묶어주기 위해서이다.

네번째 줄

로그의 성질을 이용해서 3개의 항으로 나눈다.

다섯번째 줄

\[\underbrace{\mathbf{E}_{z}[\log p_\theta(x^{(i)}|z)]}_{\text{Reconstruction}} - \underbrace{D_{KL}(q_\phi(z|x^{(i)}) || p_\theta(z))}_{\text{Regularization}} + \underbrace{D_{KL}(q_\phi(z|x^{(i)}) || p_\theta(z|x^{(i)}))}_{\text{Error (Intractable)}}\]

$\mathbf{E}[\log \frac{q}{p}]$ 형태를 KL Divergence $D_{KL}(q||p)$ 기호로 바꾼다.

• 항 1 (Reconstruction): 디코더가 $x$를 잘 복원할 확률을 올려준다.
• 항 2 (Regularization): 인코더 분포($q$)와 표준정규분포($p$) 사이의 거리를 같게만들기
• 항 3 (Error): 인코더 분포($q$)와 진짜 Posterior($p(z|x)$) 사이의 거리. 이때 인코더 부분은 구할 수 있지만, $p_\theta(z|x^{(i)})$는 intractable(계산 불가능)하다. 하지만 이 항 자체가 KL-Divergence기 때문에 0이상이라는건 보장된다.

따라서 항 3은 계산할 수 없지만 0보다 크거나 같다는게 보장되므로, liklihood를 극대화 시키기 위해서는 항1과 항2를 극대화 시키면 된다. 그리고 우리는 이것을 Variational Lower Bound 혹은 ELBO(Evidence Lower Bound)라고 부른다.

따라서 정리하자면

\[ELBO = \mathcal{L}(x^{(i)}, \theta, \phi) = \mathbf{E}_{z} \left[ \log p_{\theta}(x^{(i)}|z) \right] - D*{KL} \left( q*{\phi}(z|x^{(i)}) \parallel p\_{\theta}(z) \right)\] \[\theta^*, \phi^* = \operatorname*{arg\,max}_{\theta, \phi} \sum_{i=1}^{N} \mathcal{L}(x^{(i)}, \theta, \phi)\]

혹은 이를 뒤집어

\[\operatorname*{arg\,min}_{\theta, \phi} \sum_{i} -\mathbb{E}_{q_{\phi}(z|x_i)} \left[ \log(p(x_i | g_{\theta}(z))) \right] + KL(q_{\phi}(z|x_i) \parallel p(z))\]

* 참고 : 여기서 $\theta$는 디코더의 파라미터, $\phi$는 인코더의 파라미터를 의미한다.

위 두항의 역할을 다시 말하면

1. Reconstruction Error (복원 오차) 현재 샘플링용 함수에 대한 negative log likelihood$x_i$에 대한 복원 오차 (Autoencoder 관점)
2. Regularization (정규화) 현재 샘플링용 함수에 대한 추가 조건샘플링의 용이성 및 생성 데이터에 대한 통제성을 위한 조건을 Prior(사전 분포)에 부여하고, 학습된 분포가 이와 유사해야 한다는 조건을 부여

이 두 항을 계산하는 법은 위와 같다.

Reparameterization Trick

단순하게 인코더의 출력으로 나온 평균과 표준편차로 정규분포를 만들고, 여기서 샘플링을 하는 방식으로는 backpropagation이 안된다. 따라서 $\epsilon$을 표준정규분포에서 샘플링해서 그것을 표준편차에 곱하고 평균에 더해준 값을 샘플링 값으로 사용하면 전체적으로 미분가능해지면서 backpropagation이 가능해진다. 직관적으로 생각하면 z에 대한 식이 왼쪽에는 없이 샘플링지만, 오른쪽은 z에 대한 구체적인 식이 생기게된다.

Reference

임커밋 유튜브 VAE 영상

KAIST 강남우 교수님 VAE 영상

KAIST 성민혁 교수님 VAE 강의