CVPR 2025
SeonHwa Kim, Jiwon Kim, Soobin Park, Donghoon Ahn, Jiwon Kang, Seungryong Kim, Kyong Hwan Jin, Eunju Cha
27 Feb 2025
[paper]

preliminary

Diffusion Model and Sampling Guidance

해당 논문에서는 Diffsuion 모델 그중에서도, text to image 모델에 대해 다루고 있다.

\[\mathcal{L}(\phi) = \mathbb{E}_{t,\epsilon} \left[ \left\| \epsilon_{\phi}(\mathbf{z}_t, y, t) - \epsilon \right\|_2^2 \right]\]

첫번째로 T2I Diffusion 모델의 Loss function이다. $\phi$는 Diffusion 모델의 파라미터가 된다. 즉 Diffusion 모델의 파라미터를 최적화하는 방법을 다루고 있다.

• $z_t$ : timestamp가 t일때의 이미지, $z_0$가 원본이미지가 됨
• y : 프롬프트
• $\epsilon_\phi$ : diffusion 모델의 예측기
• $\epsilon \sim \mathcal{N}(0, I) $ : 정규분포를 따르는 랜덤 노이즈
• $t \sim \mathcal{U}(0,1)$ : uniform 분포를 따르는 시간축, 즉 0일때 원본이미지, 1일때 완벽한 정규분포 노이즈가 됨
• $||_2^2$ : L2 노름의 제곱
• $\mathbb{E}_{t,\epsilon}$ : t와 $\epsilon$을 바꾸가면서 얻은 평균을 사용한다는 뜻

\[\mathbf{z}_t = \sqrt{\alpha_t} \mathbf{z}_0 + \sqrt{1 - \alpha_t} \boldsymbol{\epsilon}\]

Diffusion 모델 forward process의 점프공식 노이즈를 조금씩 추가하는 방법으로 $z_t$를 얻어내면 마르코프체인을 통해 노이즈를 더해야하는데, 이는 매우 비효율적이므로 바로 점프해서 얻을 수 있는 공식

• $\alpha_t$ : 원본정보를 얼마나 유지할지 결정하는 계수, 보통 0 ~ 1 값임. t가 커짐에 따라 0에 가까워짐. 해당 논문에서는 nosise schedule이라 부름
• $\sqrt{\alpha_t} \mathbf{z}_0$ : 원본 이미지의 강도
• $\sqrt{1 - \alpha_t} \boldsymbol{\epsilon}$ : 노이즈의 강도
• 참고 : Diffusion 원본 논문에서 $\beta_t$를 각 단게에 추가되는 노이즈의 분산으로 정의하는데, $\alpha_t = 1 - \beta_t$ 이 관계를 만족하게됨.

\[\bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s = \prod_{s=1}^{t} (1 - \beta_s)\]

• 참고2 : 실제로 $\alpha_t$를 그냥 사용하는게 아닌 누적된 값을 사용. 이에 바를 붙인 $\bar{\alpha}_t$를 사용함. -> 타임스탬프가 0에서 t까지 옴에 따라 signal(원본정보)가 얼마나 살아남았는지의 누적 비율 을 사용

CFG 공식

\[\epsilon_{\phi}^{\omega}(\mathbf{z}_t, y, t) = (1 + \omega)\epsilon_{\phi}(\mathbf{z}_t, y, t) - \omega\epsilon_{\phi}(\mathbf{z}_t, \emptyset, t)\]

Diffusion 모델을 원하는대로 생성하기 위해서 2가지 기법이 있다. Classifier Guidance (CG)와 Classifier-Free Guidance (CFG)가 존재한다.

Classifier Guidance (CG)의 경우엔 Diffusion 모델과 더불어 이미지를 판별할 별도의 classifier 모델을 붙여, 현재 만들어지고 있는 이미지가 재대로 만들어지고 있는지 확률(liklihood)를 계산하여 classifier가 모델에게 gradient를 전달해주어, 원하는 방식으로 생성되게 유도한다. 하지만 해당 방식은 별도의 분류 모델을 학습해야 할 필요가 있고, 제한된 라벨로만 생성이 된다는 한계가 있었다.

이에 Classifier-Free Guidance (CFG)가 대안으로 제안되었고, 현재 Diffusion을 활용하는 가장 표준적으로 사용되는 방식이다. 학습할때 10 ~ 20%정도의 텍스트 프롬프트 대신 빈값($\emptyset$)를 넣고 학습시켜 모델이 텍스트를 보고 그리는 법(conditional)과 아무거나 그리는 법(unconditional)을 한 모델 내에서 동시에 학습 시키고, 추론 단계에서 모델에게 프롬프트 대로,그리고 무시하고 그린 두가지를 물어보아 두 결과의 차이를 통해 프롬프트 방향으로 좀 더 강하게 밀어붙인다. 이를 통해 별도의 분류기 없이도 더 좋은 이미지 품질을 얻을 수 있게 되었다.

위 수식에서 CFG에서 말한대로 Conditional에서 Unconditional의 차이를 빼서 수정된 그라디언트를 구하는 것을 보여준다. 여기서 $\omega$는 guidance scale로 unconditional에 가중치를 얼마나 줄 것인지를 의미한다.

Score Distillation Sampling (SDS, Dream Fusion)

\[\nabla_\theta \mathcal{L}_{\text{SDS}}(\mathbf{z}, y) = \mathbb{E}_{t,\epsilon} \left[ \omega(t) \left( \epsilon_\phi^\omega(\mathbf{z}_t, y, t) - \epsilon \right) \frac{\partial \mathbf{z}}{\partial \theta} \right]\]

DreamFusion은 구글에서 발표한 Text to 3D 생성 모델로, 2D Diffusion 모델을 통해 3D모델의 파라미터를 최적화 시키는 방법을 다루고 있다. 3D 데이터는 2D 데이터에 비해 매우 적기 때문에 강력한 2D 생성 모델(ex. Stable Diffusion)을 통해 3D 모델(NeRF)를 학습 시키는 방법을 다룬다. 이는 강력한 Diffusion 모델의 지식을 3D 모델에 distillation하는 과정으로 볼 수 있다.

• $\theta$ : 우리가 최적화 시킬 NeRF의 파라미터
• $z = g(\theta)$ : $\theta$를 통해 얻은 특정 각도에서 렌더링한 2D 이미지
• $z_t$ : 렌더링 된 이미지에 노이즈를 섞은 것
• $\epsilon_\phi^\omega(\mathbf{z}_t, y, t)$ : CFG가 적용된 Diffusion 모델이 본 프롬프트 대로 이미지가 되려면 어떤 그라디언트 방향으로 가야하는지
• $\epsilon_\phi^\omega - \epsilon$ : (학습된 Diffusion이 생각하는 프롬프트대로 되기 위한 노이즈) - (실제 노이즈) -> 현재 렌더링 된 이미지가 진짜 이미지가 되기 위해 수정되어야 할 방향
• $\frac{\partial \mathbf{z}}{\partial \theta}$ : 이미지 픽셀을 수정하기 위해 NeRF의 파라미터($\theta$)를 어떻게 수정해야하는지에 대한 미분값, 자코비안

여기서 논문의 저자는 하나의 프롬프트는 여러개의 3D volume을 의미할 수 있다고 언급한다. 예를들면 의자 라는 프롬프트는 흔들의자, 소파 등 다양한 의자에 대응 될 수 있고 이는 결과를 흐리게 만드는 원인이 될 수 있다.

Delta Denoising Score (DDS)

\[\nabla_{\theta} \mathcal{L}_{\text{DDS}} = \mathbb{E}_{t, \epsilon} \left[ \left( \epsilon^{\omega}_{\phi} \left( \mathbf{z}^{\text{trg}}_t, y^{\text{trg}}, t \right) - \epsilon^{\omega}_{\phi} \left( \mathbf{z}^{\text{src}}_t, y^{\text{src}}, t \right) \right) \frac{\partial \mathbf{z}^{\text{trg}}}{\partial \theta} \right]\]

DDS는 SDS와 달리 이미지 편집에 특화된 기술로 무에서 유를 창조하는게 아닌, 기존 이미지에서 원하는 부분만 바꾸기 위한 기술이다.

기존의 SDS의 노이즈는 무작위 가우시안 노이즈를 빼줌으로인해 이미지 구조 정보가 반영되지 않는다. 따라서 무작위 노이즈 대신 원본 이미지에 대한 예측값을 빼주자라는 발상에서 나온 아이디어이다.

가장 단순하게 생각하면 이미지 편집에서 src이미지에서 바뀌지 않는 부분은 $\epsilon^{trg}_\phi$이 $\epsilon^{src}_\phi$와 같게 되면서 실제로 수식에서 그라디언트가 0이된다.

Fixed-point Iteration

\[x_{n+1} = f(x_n), \quad n = 0, 1, 2, \dots\]

Fixed point란 함수에 넣은 입력값이 그대로 출력되는 지점을 말하며 f(x)에 x를 넣어도 다시 x가 나오므로 fixed 되었다고 볼 수 있다.

이 계산을 하는 이유는 Diffusion 모델은 노이즈를 제거하는 비선형 함수 인데, 이를 저렴한 연산으로 계산할 수 있기에 때문이다.

Background

\[\mathbf{z}_{0|t}^{\text{src}} = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{z}_t^{\text{src}} - \sqrt{1 - \alpha_t} \epsilon_\phi^{\text{src}} \right)\]

논문의 저자는 $\epsilon_{\phi}^{src}$에 $z^{src}$(원본이미지)가 얼마나 포함되었는지 확인해보았다. 이를 위해 위 수식을 통해 posterier mean을 계산한다.

여기서 posterier mean은 위 Forward Process 공식에서 유도할 수 있으며, 여기서 진짜 노이즈 $\epsilon$을 모르기 때문에 이는 원본이 아니라 추정된 원본이 되는 것이다. 즉 posterier mean은 timestamp가 t일때 추정한 원본의 값이 된다.

위 이미지에서는 t가 증가함에 따라 $z^{src}$에서 posterier mean을 구하기 어렵다는 것을 보여준다. 그리고 이는 $\epsilon^{src}_{\phi}$가 $z^{src}$에 완벽하게 부합하지 않는다는 것을 의미하고, 이 $\epsilon_{\phi}^{src}$가 수정될 필요가 있음을 의미한다.

또한 만약 DDS loss가 정확하여, guidance가 재대로 작동했다면 $z^{src}$에서 $z^{trg}$로 변환시켜다가 다시 $z^{src}$로 재구성이 잘 되어야 할 것이다. 하지만 위 사진을 보면 원본이미지로 돌아가는게 정확하지 않고, 이는 $\epsilon_{\phi}^{src}$가 $z^{src}$에 부합하지 않음을 다시한번 보여주며, 주입된 노이즈 $\epsilon$과 $\epsilon_{\phi}^{src}$의 차이인 에러가 점점 누적됨에 의해 발생한다.

위위 사진에서 노이즈가 추가된 타임스탬프가 짧을수록 posterier mean과 유사한 모습을 보였기에, 저자는 누적된 오류가 타임스탬프가 길어짐에 따라 생긴것일 수도 있다고 생각하여 $t$ ~ $\mathcal{U}(0,0.2)$와 $t$ ~ $\mathcal{U}(0,1)$을 비교해본다. 그 결과 0.2로 뒀을때 비현실적이고 과장된 구조를 보여준다. 이는 t를 제한하는 것만으로는 부족하고 근본적인 해결책이 필요하다는 것을 의미한다.

Methodology

\[\mathcal{L}_{\text{FPR}} = d(\mathbf{z}^{\text{src}}, \mathbf{z}_{0|t}^{\text{src}})\]

그래서 저자는 $\epsilon_{\phi}^{src}$를 $z^{src}$에 맞추기 위한 Fixed point Regularization을 제안한다. 여기서 기본 전제는 $\epsilon^{src}_{\phi}$가 $z^{src}$를 예측하기 위한 gradient를 잘 예측한다면, posterier mean 또한 $z^{src}$에 대한 충분한 정보를 포함하고 있을 것이라는 것이다.

따라서 FPR의 Loss는 posterier mean와 $z^{src}$의 차이를 통해 계산되며 여기서 차이를 구하기 위해서 유클리드 거리를 사용했다고 한다.

\[\mathbf{z}_t^{\text{src}} \leftarrow \mathbf{z}_t^{\text{src}} - \lambda \nabla_{\mathbf{z}_t^{\text{src}}} \mathcal{L}_{\text{FPR}}\]

여기서 FPR을 통해 $z_t^{src}$와 $\epsilon$을 수정하는 방법을 통해 $\epsilon_{\phi}^{src}$를 조작할 수 있는데 실험을 통해 저자는 $z_t^{src}$를 조작하는 방법을 선택하였고 위 수식과 같이 $z_t^{src}$를 업데이트한다. 여기서 $\lambda$는 정규화 계수이다. 여기서 위 수식은 경사하강법이랑 수식이 비슷하므로 경사하강법처럼 최적화를 진행한다라고 생각하면된다.

\[\epsilon^* = \frac{1}{\sqrt{1 - \alpha_t}} \left( \mathbf{z}_t^{\text{src*}} - \sqrt{\alpha_t} \mathbf{z}^{\text{src}} \right)\]

여기서 FPR을 통해 최적화된 $z_t^{src*}$를 통해 수정된 $\epsilon^*$을 얻을 수 있고

\[\nabla_\theta \mathcal{L}_{\text{IDS}} = \mathbb{E}_{t,\epsilon} \left[ \left( \epsilon_{\phi}^{\omega} \left( \mathbf{z}_{t}^{\text{trg*}}, y^{\text{trg}}, t \right) - \epsilon_{\phi}^{\omega} \left( \mathbf{z}_{t}^{\text{src*}}, y^{\text{src}}, t \right) \right) \frac{\partial \mathbf{z}^{\text{trg}}}{\partial \theta} \right]\]

DDS에서 *가 붙은 부분이 수정되어 최종 수식이 나오게 된다.

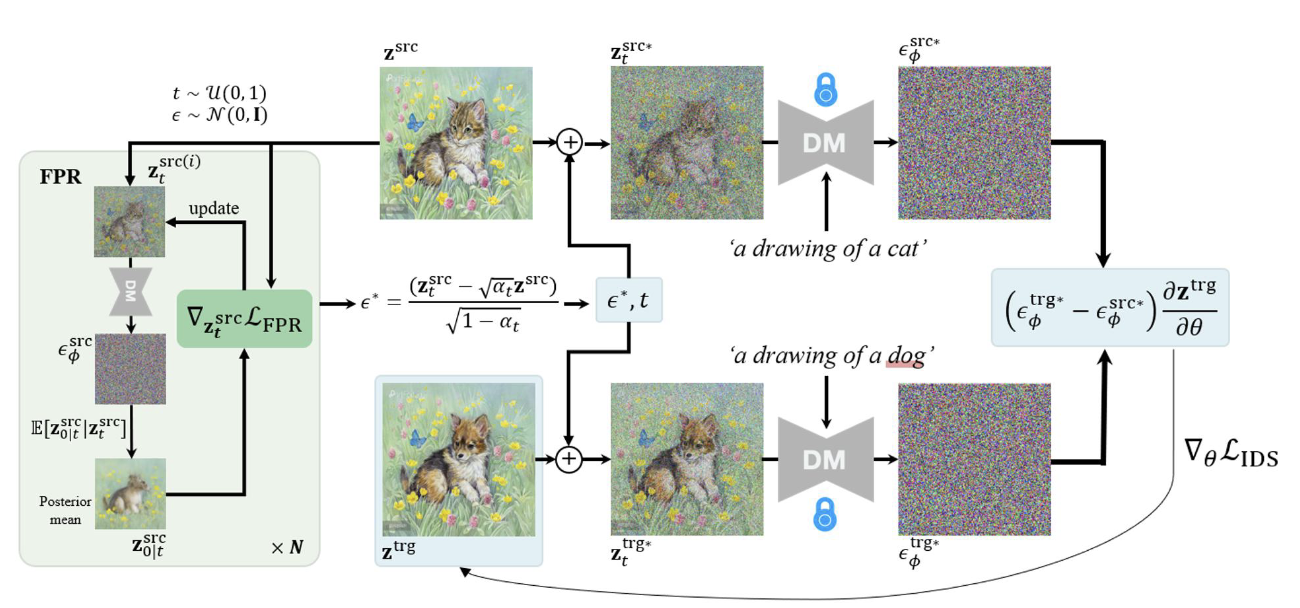
이제 전체적인 overview를 보자. $z^{src}$로부터 Forward Process로 노이즈를 추가하고, FPR Loss를 계산하여 반복하여 $z_t^{src}$를 업데이트한다. 그리고 그 이후 이를통해 역으로 계산한 $\epsilon^*$를 통해서 DDS와 같은 방식으로 이미지 편집을 진행하게 된다.

Experiment

text-guided image editing

4가지 SOTA 모델과 텍스트 이미지 편집성능을 비교한다. 정량적 결과는 생략

Editing NeRF

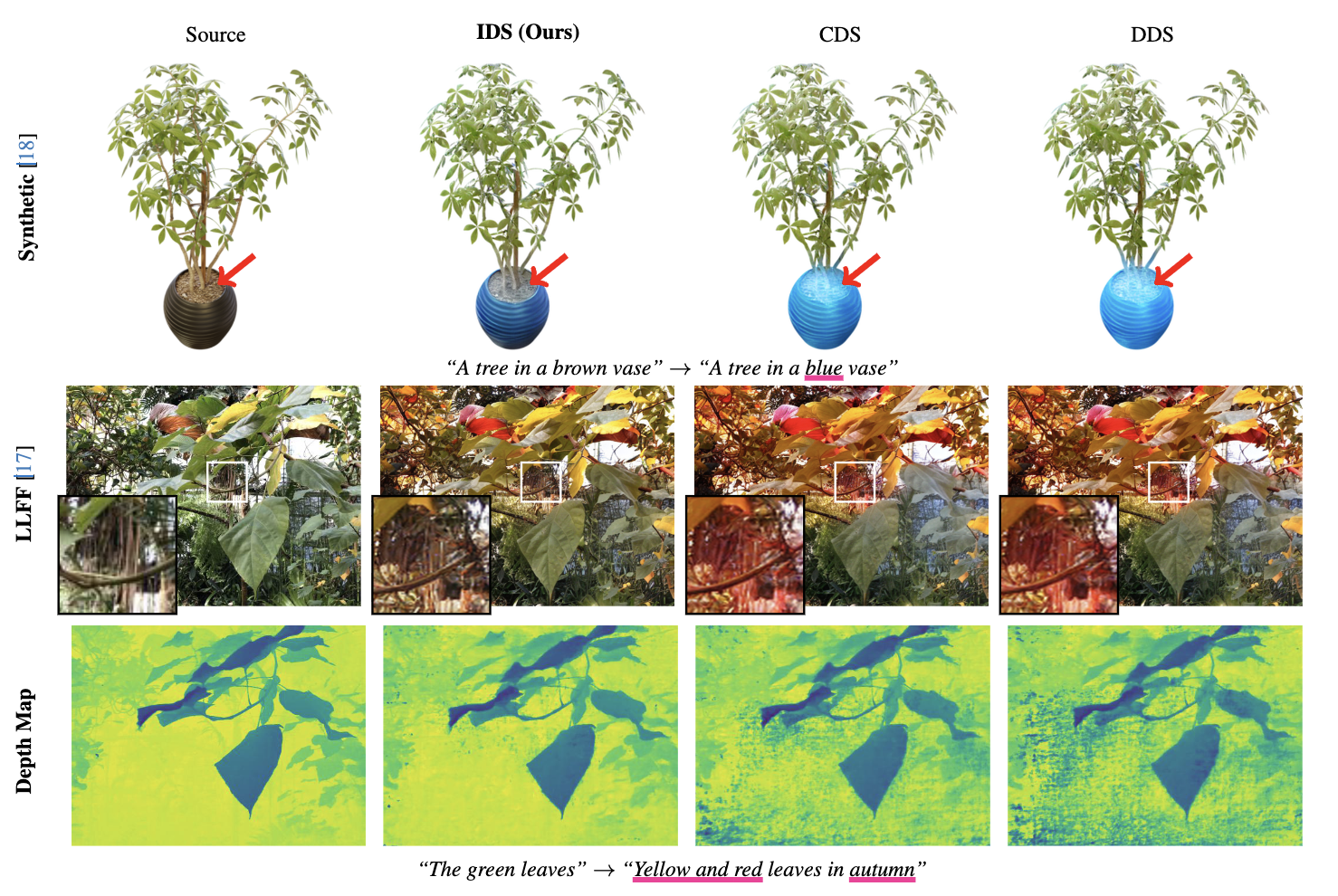
NeRF를 수정하는 케이스, 첫번째 행에서 화병 색을 바꾸는 상황에서 나머지 모델들은 흙의 색까지 바꾸지만 IDS는 그러하지 않는다. 두번째 행에서는 잎의 색과 분위기를 바꾸는 상황인데, 이때 나머지 모델은 줄기까지 바꿨지만 IDS는 그러지 않았다. 마지막행은 depth maps인데 이미지 편집 이후에도 노이즈가 적은 깨끗한 depth map을 보여준다.

Ablation Study

Ablation Study를 통해서 $\lambda$값이 $z_{src}$정보를 얼마나 보존시키는지를 보여준다.