ICCV 2025
Jiwon Kim, Pureum Kim, SeonHwa Kim, Soobin Park, Eunju Cha, Kyong Hwan Jin
13 Aug 2025
[paper]

preliminary

Controllable Text-to-Image diffusion

이파트에서는 총 3가지 Text to Image 모델에 대해 언급한다.

ControlNet

학습된 T2I Diffusion 모델에 spatial conditional control를 더해 유저가 포즈나, 레이아웃 등에서 강력한 제어가 가능해짐. 하지만 여러 모델 파인튜닝이 필요하여 학습 오버헤드가 높았다.

FreeControl

T2I Diffusion 모델에 추가적인 학습이 필요 없이도, 이미지 생성에서 잘 생성된다. 하지만 loss를 줄이기 위해 latent space의 gradient 조작에 의지하므로 컴퓨팅 리소스를 많이 먹는다.

Ctrl-X

더 빠르고 가벼운 T2I 연산을 위해 제안되었으며, diffusion 모델에 Structure 이미지와 Appearance 이미지를 따로 diffusion에 넣게된다. 여기서 특징이 diffusion 모델의 feed forward는 Structure가 담당하고, Self Attention은 Appearance가 담당하게 된다. 이를 통해 같은 카테고리에 있는 두 이미지를 통해 이미지 생성이 잘되었지만, 클래스가 다른 sturcture와 appearance가 있는 상황에서는 안좋은 결과를 보이게 된다.

Score distillation sampling

Score distillation sampling (SDS), Delta De-noising Score (DDS), Identity-preserving Distillation Sampling (IDS)는 IDS 논문 리뷰 참고

Methodology

그래서 여기서 해결하고자하는 문제는 Ctrl-X에서 포즈나 레이아웃을 재대로 포착하지 못하는 것을 해결하는 것이다.

Notation

Dual Recursive Feedback

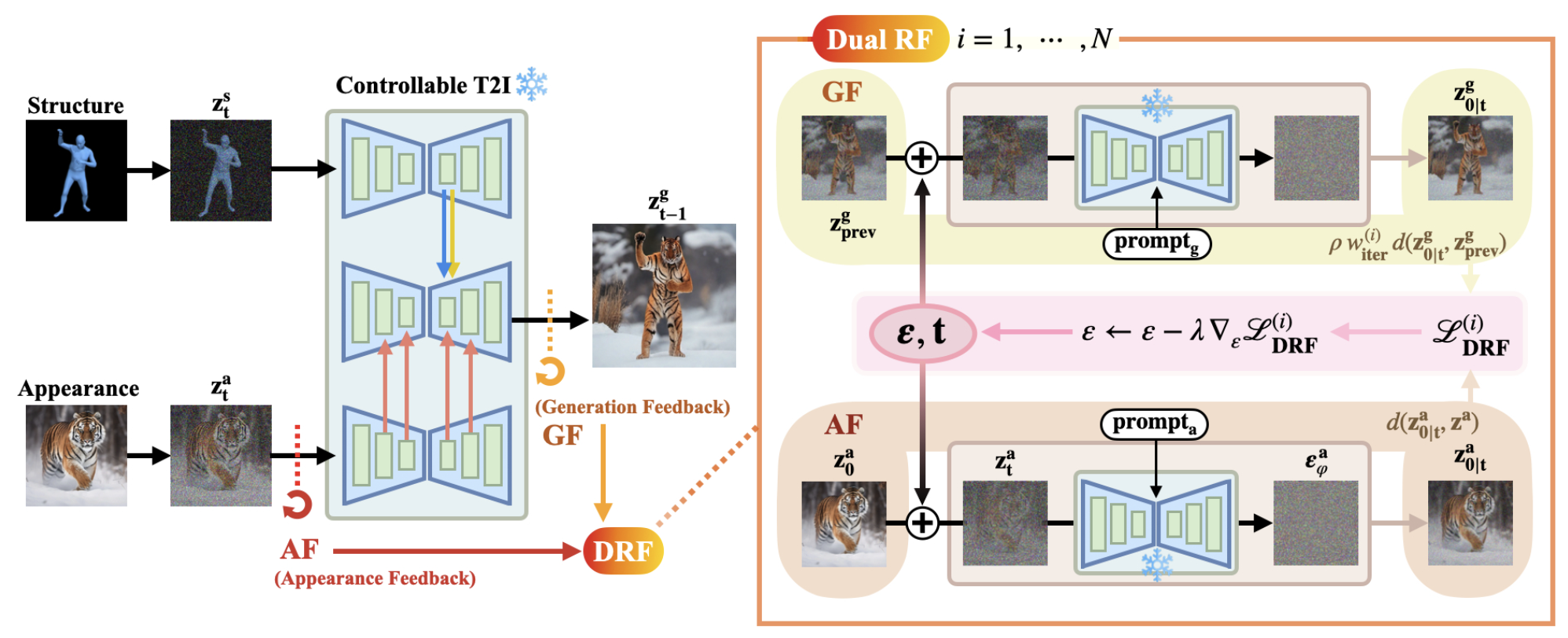
우선 flow chart에서 $I^a$와 $I^s$를 집어 넣어 $z^g$를 얻어내게 되는데 위에서 언급했듯, Ctrl-X를 기반으로 한 구조이기에 $A_{t}^{s}$가 structure 정보를 $h_{t}^{a}$가 appearance 정보를 갖게되고, 이 디노이징 단계를 수식으로 표현하며 아래와 같다.

\[\boldsymbol{z}_{t-1}^{g} = \text{Ctrl-X}(\boldsymbol{z}_{t}^{g} \mid t, y, f_{t}^{s}, A_{t}^{s}, h_{t}^{a})\]

여기서 저자는 $I^a$와 $I^s$의 클래스가 다르다면 단순히 appearace와 structure를 나누는것만으로는 $I^g$에 두 특징을 반영하기 어렵다고 하고 있다. 위 사진에서 제일 오른쪽 사진을 보면 두 정보가 재대로 반영되지 않는 것을 볼 수 있다. 그래서 저자는 이걸 해결하기 위해 $z^g$가 생성될때동안 score guidance를 활용하는 Dual Recursive Feedback을 제안한다.

Appearance Feedback

FreeControl과 Ctrl-X의 appearance 부족문제를 해결하기 위해 appearance의 gradient를 보아야하는데 이는 IDS에서처럼 $\epsilon_\theta^a$가 $z_t^a$를 $z^a$로 만들어주는 것을 보장하지 못한다. 따라서 여기서 fixed point라는 개념을 도입한다.

하지만 IDS는 uniform한 타임스탬프에서 랜덤하게 샘플링하는데, 큰 타임스탬프에서 얻게되는 posterier mean은 $z_0^a$의 정보를 충분하게 갖지 못한다. 따라서 DRF에서는 타임스탬프를 1에서 0까지 줄여가며 결과를 얻어내게 된다.

\[\tilde{\mathbf{z}}_t^a = \sqrt{\frac{\alpha_t}{\alpha_{t-1}}} \mathbf{z}_0^a + \sqrt{1 - \frac{\alpha_t}{\alpha_{t-1}}} \boldsymbol{\epsilon}\]

위 수식은 $z_0^a$와 posterier mean의 차이를 보정하기 위해 기존의 diffusion forward수식을 다음과 같이 수정하였다. 기존의 $\alpha_t$는 곱해지는 누적값이라 t가 커짐에 따라 0에 근사해져 원본정보가 거의 사라지게 된다. 따라서 $\alpha_{t-1}$로 나눠줌으로 원본이미지 형태가 남아있을 수 있게된다 ($z_0^a$ 앞의 계수가 1에 가까워지므로). 위 다람쥐 사진에서 4열이 기존 forward 공식을 썼을때, 3열이 DRF 수식을 썼을때의 결과라고 한다.

\[\mathcal{L}_{\text{app}} = d(\mathbf{z}_{0|t}^{a}, \mathbf{z}_{0}^{a}),\]

그래서 IDS와 마찬가지로 원본과 수정된 $\tilde{\mathbf{z}}_t^a$로 부터 얻은 posterier mean의 차이를 줄이는 방식으로 loss함수가 설계되었다.

Generation Feedback

\[\mathcal{L}_{\text{gen}} = d(\mathbf{z}_{0|t}^g, \mathbf{z}_{\text{prev}}^g)\]

저자는 appearance의 오버피팅을 막기 위해 $z^g$에 generation feedback를 도입한다. 여기서 score $\epsilon_\theta^g$는 $z_{prev}^g$에 의해 매번 업데이트 되는데, $z_{prev}^g$를 기준점으로 하여 바로 이전에 생성된 gradient에서 크게 벗어나지 않게 한다.

Dual Recursive Feedback

위에 있는 두개의 appearance feedback과 generation feedback의 loss를 이용해 최종 Dual Recursive Feedback를 계산한다. 이때 초반에 랜덤 가우시안 노이즈에서 얻게되는 latent는 structual 정보를 반영하지 못할 수 있어서, DRF의 경우 초기 5 step 이후에 20 step에 적용시켰다고 한다.

\[w^{(i)}_{\text{iter}} = \sqrt{\frac{\exp\left( k \frac{i}{N-1} \right) - 1}{\exp(k) - 1}}\]

처음에는 appearance가 더 중요하고, 반복횟수가 올라감에 따라 generatiion feedback이 더 중요해진다. 따라서 appearance와 generative feedback의 균형을 위해, 점점 generation feedback의 가중치를 증가시켜주기 위해 위와같은 가중치를 준다.

\[\mathcal{L}_{\text{DRF}}^{(i)} \leftarrow d(\mathbf{z}_{0|t}^{a}, \mathbf{z}_{0}^{a}) + \rho w_{\text{iter}}^{(i)} d(\mathbf{z}_{0|t}^{g}, \mathbf{z}_{\text{prev}}^{g})\]

그래서 최종 DRF의 Loss function은 다음과 같이 정의되며 $\rho$는 하이퍼파라미터이다.

\[\epsilon \leftarrow \epsilon - \lambda \nabla_\epsilon \mathcal{L}^{(i)}_{\text{DRF}}\]

여기서 노이즈 $\epsilon$은 $z_{t-1}^g$와 $z^a$에 더해져 $z_t^g$와 $\tilde{\mathbf{z}}_t^a$를 만들며, 이는 geneation과 appearance 사이의 연결점이라고 볼 수 있다. 따라서 IDS와 달리 위 공식과 같이 노이즈 자체를 최적화해 최적의 노이즈를 구해낸다. 이 노이즈를 이용하여 보완된 generative latent를 얻을 수 있다.

DRF의 수도코드는 다음과 같다.