[논문리뷰 / PNAS 2006] Modularity and community structure in networks
PNAS 2006. [Paper]
MEJ Newman
University of Michigan
17 Feb 2006
Introduction
많은 과학 시스템은 네트워크로 표현이 가능합니다. 네트워크란 node 혹은 vertices(정점)으로 구성된 그래프를 의미한다. 대표적으로 인터넷 WWW, 생물학적 네트워크(metabolic network), 뉴럴네트워크, 소셜 네트워크 등이 있습니다.
수십년동안 많은 연구들이 있었지만 대규모 데이터의 접근이 가능해지면서 네트워크에 대한 연구가 급증하였습니다. 이러한 연구들에서 통계적인 분석을 통해 얻어낸 네트워크의 구조적인 특징은 다음과 같습니다.
- high network transitivity : 네트워크 노드들끼리 삼각형으로 연결되는 패턴이 있음
- power-law degree distributions : 노드의 연결 차수(degree)가 특정 패턴을 따름
- repeated local motifs : 네트워크에서 특정 구조가 반복됨
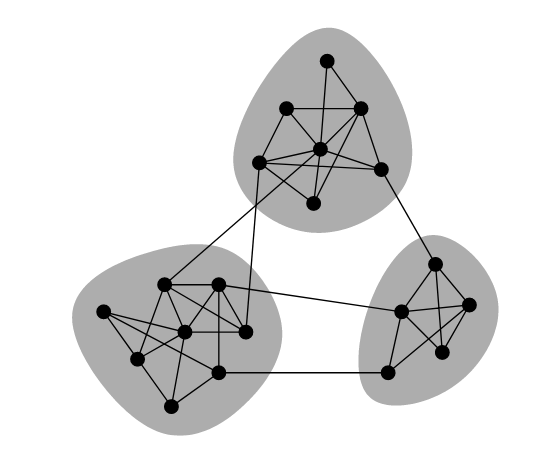
우선 Community Structure가 어떻게 되는지 정의해야합니다. 해당 논문에서는 이를 그룹의 vertices사이엔 밀집한 연결이 있고, 각 그룹 사이에는 희소한 연결이 있는 것으로 정의합니다. 따라서 위 figure를 보면 3개의 그룹이 존재하고, 각 그룹 사이에는 밀집한 연결이 존재하지만 각 그룹사이에는 연결이 많지 않음을 알 수 있습니다. 이 논문에서는 그룹을 커뮤니티라는 말로 자주 표현됩니다.
우리는 네트워크에서 community를 detection하는거에 관심이 있습니다. 이는 다음과 같은 community detection을 하는 이유는 다음과 같습니다. 우선 웹 네트워크에서는 관련된 주제의 웹페이지 그룹을 찾을 수 있습니다. 또한 소셜 네트워크에서는 사회적 집단이나 커뮤니티를 감지할 수 있습니다. 그리고 생물학적 네트워크에서는 각 모듈이 다른 기능을 수행할 때 모듈이 어떻게 동작되는지를 볼 수 있습니다.
기존에는 총 2가지 종류의 community detection 방법이 존재합니다. 각 방법은 같은 질문에 대한 접근 방법을 제공하지만 차이가 존재합니다.
- graph partitioning : 일반적으로 Computer Science나 관련 분야에서 사용하고, 병렬 컴퓨팅, VLSI 설계 등에서 활용됨, 사전에 그룹의 수를 알때 사용됨. 일단 네트워크가 잘 나뉘지 않아도 무조건 분할을 시도
- community structure detection(= block modeling, hierachical clusturing) : 주로 사회학자나 물리학자 등들에 의해 사용하며 소셜 네트워크나 생물학적 네트워크에 사용됨, 그룹의 수를 모르더라도 적용 가능함. 다른 사람의 개입 없이 네트워크 자체만으로 그룹의 수가 결정됨.
해당 논문에서는 현실 세계의 시스템을 표현한 데이터셋의 Community Structure Detection을 하는데 집중합니다. 그리고 해당 논문에서는 위에 언급된 두 community detection 방법의 유사점과 차이점을 바탕으로 기술된다고 합니다.
The method of optimal modularity
일단 우리는 네트워크를 자연스럽게 겹쳐지지 않는 커뮤니티로 분할하는 community detection을 확인할겁니다.
우선 네트워크 가장 쉬운 방법으로 두개의 커뮤니티로 나누는 케이스를 생각해봅시다. 이때는 네트워크의 두 그룹 사이의 edge를 최소화 하는 두 group을 구하면 되지 않을까요? 이런 방법를 minimum cut방식이라고 하며 graph partitioning 관련 논문에서 빠짐없이 등장합니다.
하지만 위에서 언급됐든 community detection은 사전에 그룹의 수를 모를 수 있습니다. 가장 극단적으로 두그룹중 하나의 그룹에 모든 vertices를 넣는다면 edge는 0이므로 최적인것 처럼 보이지만 community structure를 전혀 반영하지 못한 것임을 알 수 있습니다.
따라서 실제로 네트워크의 좋은 분할은 두 커뮤니티 사이에 edge가 예상보다 적은 경우를 의미합니다. 랜덤한 네트워크랑 비교할 때 두 커뮤니티 사이에 edge가 더 적거나, 커뮤니티 내의 edge가 더 많다면 이는 community structure에 있다고 볼 수 있겠죠.
이 개념을 통해 네트워크의 community structure는 edge가 통계적인 방식으로 배치된 것을 의미합니다. 그리고 우리는 이것을 Modularity(Q)라는 지표로 community structure를 정량화 합니다. (true community structure in a network corresponds to a statistically surprising arrangement of edges, can be quantified using the measure known as modularity) Modularity는 커뮤니티 내 존재하는 edge 수에서 랜덤한 네트워크에서 기대되는 edge 수를 뺀 값으로 정의됩니다.
당연하겠지만 Modularity의 값은 양수 일때 유의미한 community structure가 존재할 가능성이 높고, 음수일때 community structure가 존재할 가능성이 낮습니다. 따라서 저희의 목표는 높은 Modularity 값을 갖는 community devision을 찾는것이 목표입니다.
Danon et al.은 simulated annealing 기법을 통해 modularity를 극대화하는 실험을 진행했고, 기존의 모든 community detection보다 뛰어난 성과를 얻었다고 합니다. 하지만 simulated annealing은 계산 비용이 너무 많이 소모되어 그리디 알고리즘이나 extremal optimization(최악 요소를 교체하며 최적화)하는 방법을 통한 대체 방법이 나왔습니다.
여기서 저자는 Modularity를 spectral properties를 통해 재구성한 방법을 제시합니다. 여기서 spectral properties는 행렬의 eigenvalues와 eigenvector를 통한 방법을 의미합니다.
모듈러리티(Modularity) Q 수식
\[Q = \frac{1}{4m} \sum_{ij} \left(A_{ij} - \frac{k_i k_j}{2m}\right) s_i s_j = \frac{1}{4m} \mathbf{s}^T \mathbf{B} \mathbf{s}\]- Q : Modularity
- m : 네트워크의 총 edge의 수($m = \frac{1}{2} \sum_i k_i$)
- $k_i$ : 노드 i의 차수
- $A_{ij}$ : adjacency matrix(인접행렬)의 요소, 즉 i와 j사이의 edge의 수
- $A_{ij} = 1$ 이면 서로 연결, $A_{ij} = 0$ 이면 연결이 없음. 다만 다중연결로 인해 1보다 더 클 수 있음
- $\frac{k_i k_j}{2m}$ : 무작위 네트워크에서 기대되는 i와 j 사이의 edge의 수
- $s_i, s_j$ : 노드 i와 j가 속한 커뮤니티 정보를 담는 변수
- $s_i = 1$ 이면 노드 i는 첫 번째 그룹에 속함
- $s_i = -1$ 이면 노드 i는 두 번째 그룹에 속함
- 즉 $s_is_j$는 두 노드가 같은 그룹에속하면 1, 다른 노드에 속하면 -1
- $s$ : 여기서 s는 각 노드의 커뮤니티 정보를 나타냄
- $B$ : Modularity Matrix
- $B_{ij} = A_{ij} - \frac{k_i k_j}{2m}$
- 대칭행렬으로 모든 각 행과 열의 요소를 더하면 0임
- 위 성질로 B의 eigenvector는 (1,1,1,…)가 되고 eigenvalue는 0이 됨
이 수식 맨 앞 $\frac{1}{4m}$은 conventional(관습적)인 표현으로 이전 modularity 정의 호환성으로 붙이는 겁니다. 그리고 그 뒤에 있는 $\left(A_{ij} - \frac{k_i k_j}{2m}\right) s_i s_j$ 부분의 경우 실제 edge 수에서 무작위 네트워크의 기대 edge 수를 뺀 값에, 커뮤니티 소속에 따른 가중치를 부여하여 값을 계산하게 됩니다.
그리고 그 뒤에 있는 수식은 이중합을 행렬곱의 형태로 변환한 것입니다. 이를 통해 뒷식부터는 행렬적인 연산을 통해 계산할 수 있게 되고, eigenvalues나 eigenvector를 활용한 기법들을 사용할 수 있게됩니다.
여기서 행렬 B는 위에서 말했듯 eigenvactor와 eigenvalue가 위와 같은 형식인데, Graph Laplacian도 동일한 특성을 갖고 있고 graph partitioning, spectral partitioning의 핵심 요소라는 유사점이 있다. 다만modularity matrix는 spectral method를 사용하지만 목표가 community detection이라는 차이가 있다.
\[Q = \sum_i a_i \mathbf{u}_i^T \mathbf{B} \sum_j a_j \mathbf{u}j = \sum_{i=1}^n (\mathbf{u}_i^T \cdot \mathbf{s})^2 \beta_i\]논문에는 위 식이 제공되어 있다. 해당 수식의 전개과정에 대해 좀 더 자세히 봐보자
전개과정
이제 $\frac{1}{4m} \mathbf{s}^T \mathbf{B} \mathbf{s}$ 식을 변환합니다. 우선 행렬 B의 normalized eigenvectors $u_i$를 통해 s를 $\mathbf{s} = \sum_{i=1}^n a_i \mathbf{u}_i$ 다음과 같은 선형 결합형태로 나타낼 수 있습니다. $a_i$는 선형결합 계수값으로 $a_i = \mathbf{u}_i^T \mathbf{s}$ 다음과 같이 정의됩니다.
\[Q = \sum_i a_i \mathbf{u}_i^T \mathbf{B} \sum_j a_j \mathbf{u}_j = \sum_i \sum_j \Bigl(a_i a_j\Bigr)\, \mathbf{u}_i^T \mathbf{B} \mathbf{u}_j\]이를 위의 Q의 행렬표현에 대입하면 다음과 같은 꼴이 되겠죠. 그리고 그 뒤에는 스칼라 값인 $a_i$를 앞으로 빼주면 위 식과 같은 형태로 표현됩니다.
여기서 고유벡터 끼리는 서로 직교 하므로 \(\mathbf{u}_i^T \mathbf{u}_j = \delta_{ij}\) 성질을 만족하고 ($\delta_{ij}$는 크로네커 델타로 $i = j$ 일 때 1, 아닐 때 0)
\[\mathbf{u}_i^T \mathbf{B} \mathbf{u}_j = \beta_i \delta_{ij}\]를 수식에 대입하면
\[\sum_i \sum_j a_i a_j \beta_i \delta_{ij}\]임.
여기서 크로네커 델타의 성질을 이용하면
\[\sum_i a_i^2 \beta_i\]만 남음. 그리고 위에서 $a_i = \mathbf{u}_i^T \cdot \mathbf{s}$는 위에서 이미 정의된 값이므로 대입하면
\[\sum_i a_i^2 \beta_i = \sum_{i=1}^n (\mathbf{u}_i^T \cdot \mathbf{s})^2 \beta_i\]가 됨. (참고로 $\frac{1}{4m}$은 간결함을 위해 생략)
본문 내용
그래서 위에서 언급 됐듯 $\beta_i$는 B의 eigenvalue, $u_i$는 B의 eigenvactor가 된다. 여기서 eigenvalue는 B의 중요도를, eigenvactor는 해당 값의 방향을 나타내게 된다.
이때 고유값은 한개가 아니라 여러개일 수 있기 때문에 $\beta_1 \geq \beta_2 \geq … \geq \beta_n$ 다음과 같이 내림차순으로 정렬했을 때 $\beta_1$이 가장 중요한 방향을 나타냄. 우리의 목표는 Q를 극대화 하는 것이기에 벡터 s를 $u_1$에 가깝게 설정해야함.
그래서 만약 다른 제약 조건이 없다면 s를 $u_1$에 비례하도록 설정하면 $s = cu_1$꼴로 표현 가능하고, 위 식에서 나머지 항들이 전부 0이 되면서 $Q = (u_1^T s)^2 \beta_1$만 남게 된다.
하지만 실제로는 s의 값은 ±1로 제한됨. 이는 두 노드가 두 네트워크 중 하나에 속한다는 것을 의미하는데, 이때문에 s가 $u_1$에 그냥 비례하게 만들 수가 없어 이를 최적화 할때 복잡도가 매우 올라감. 이의 복잡도는 가능한 모든 s의 값을 탐색해야하므로 계산시간이 exponential 하게 늘어 이는 NP-hard임. 따라서 이를 계산하기 위해선 approximate method를 활용해야함.
그래서 여기서 최적해에 가까운 sub-optimal 결과를 얻는 Spectral Partitioning을 사용한다고 함. 해당 방법에서는 가장 큰 eigenvalue를 극대화 하고 나머지는 무시함. 즉 s가 $u_1$에 완벽하게 평행하게 만들 순 없지만 $\beta_1$를 극대화하려고 시도해볼 수 있음.
\[s_i = \begin{cases} +1 & \text{if} \ (u_1)_i > 0 \\ -1 & \text{if} \ (u_1)_i < 0 \end{cases}\]구체적인 방법으로 부호를 통한 분할을 시도함. $u_1$의 요소가 양수면 첫번째그룹, 음수면 두번째 그룹으로 보는 것이다. 이방법의 장점은 커뮤니티 크기를 미리 알 필요가 없다는 점과 모든 노드가 하나의 그룹에 들어가는 것을 방지할 수 있다.이는 행렬 B가 eigenvactor $(1, 1, 1, …)^T$ 와 eigenvalue 0을 갖는데, 해당 eigenvactor가 다른 eigenvactor와 직교하기에, 만약 양의 eigenvalue가 존재한다면 해당 네트워크는 최소한 두개의 커뮤니티가 존재한다고 볼 수 있는 것이다.
이때 모든 eigenvalue가 0또는 음수라면 가장 큰 eigenvalue는 0이다. 이 경우 모든 노드가 하나의 그룹에 속하는 것이기 때문에 Q가 0 이하가 되어 더이상 modularity를 증가시킬 방법이 없으며 이는 최적의 상태임을 나타냄. 해당 상태의 네트워크를 indivisible이라고 하고, 다시말해 modularity matrix가 양의 eigenvalue가 없는 상태이다.
해당 알고리즘의 중요한 점은 네트워크를 무조건 나누지 않고, 만약 모든 eigenvalue가 0이하라면 나누지 않는게 더 낫다는 것을 인식해 의미없는 분할을 방지하고 modularity는 극대화할 수 있는 장점이 있다.
위 알고리즘에서는 부호만 고려했지만 크기(magnitude) 또한 중요한 정보를 전달한다. 크기가 큰 요소는 modularity에 큰영향을, 크기가 작은 요소는 Modularity에 작은 영향을 미친다. 즉 요소의 크기는 vertices가 해당 커뮤니티에 얼마나 강하게 속해 있는지를 의미한다. 그리고 만약 크기가 0에 가깝다면 두 커뮤니티의 경계에 있을 가능성이 높다. 해당 노드는 다른 그룹으로 이동시켜도 Q에 큰 영향을 끼치진 않는다. 해당 정보를 통해 알고리즘은 단순하게 vertices를 커뮤니티로 나누는데 그치는게 아닌, 얼마나 그 커뮤니티에 속하는지를 알려준다.
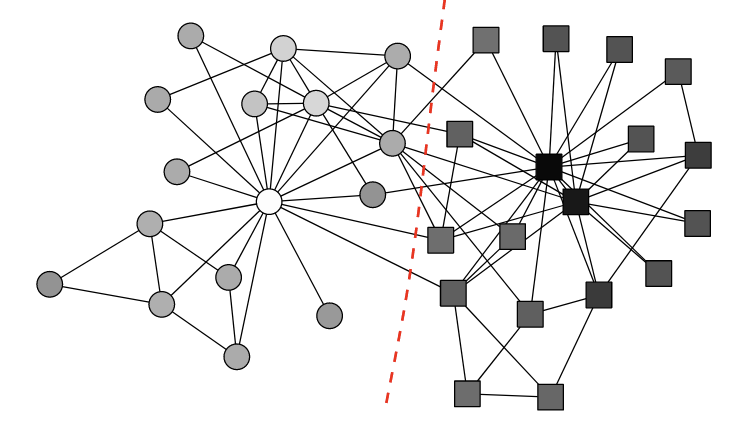
위 이미지는 Karate Club Network에 해당 알고리즘을 적용한 결과를 보여준다. 해당 네트워크는 친구관계를 바탕으로 네트워크가 구성되었으며, 두 그룹으로 나뉜걸 커뮤니티 감지 알고리즘의 표준 데이터셋으로 자주 사용됩니다.
해당 알고리즘을 적용한 결과 실제 클럽 분열 상황과 일치했으며, 위 figure에서 node의 색상은 eigenvactor의 magnitude를 바탕으로 결정된 것입니다. 양수값일 수록 하얗고, 음수값일 수록 검정에 가깝게 표시가 된것을 알 수 있고 가장 강한 양수와 음수 값을 갖는 3명이 두 그룹의 주요리더에 해당되며, 커뮤니티의 영향력도 표시할 수 있음을 알 수 있다.
Dividing networks into more than two communities
위에서는 커뮤니티를 2개의 커뮤니티로 나누는 방법에 대해 이야기했으니, 이제 네트워크를 두 개보다 많은 커뮤니티로 나누는 방법에 대해 생각해봐야 합니다.
가장 직관적으로 생각할 수 커뮤니티를 2개로 나눈후, 나눠진 커뮤니티로부터 동일한 알고리즘으로 반복적으로 적용해 네트워크를 분할해 여러 커뮤니티를 얻을 수 있습니다. 이때 두 그룹으로 나눈 다음에 두 그룹 사이의 edge를 삭제하고 다시 서브그래프에 대해 알고리즘을 적용할 수 있습니다. 근데 해당 방법을 사용하면 위 1번 수식에서 사용되는 degree에 영향을 주어 Modularity Matrix의 값에도 영향을 주어 잘못된 modularity값을 극대화 할 수 있고, 정확한 커뮤니티 감지가 불가능합니다.
\[B_{ij}^{(g)} = A_{ij} - \frac{k_i k_j}{2m} - \delta_{ij} \left[ k_i^{(g)} - k_i \frac{d_g}{2m} \right]\]- $d_g$ : 서브그래프 g 내 모든 노드의 차수의 합
- $d_g = \sum_{i \in g} k_i$
- $k_i^{(g)}$ : 서브그래프 g내의 노드 i의 차수
- $k_i \frac{d_g}{2m}$ : 전체네트워크 차수를 서브그래프의 정규화 차수된로 변환한 것
그래서 위와 같이 새로 생긴 서브그래프 g에 대한 Modularity Matrix $B^{(g)}$ 를 별도로 정의합니다. 해당 수식은 modularity matrix 수식에서 뒤에 보정을 해주는 수식이 추가된겁니다. 해당 수식은 서브그래프로 변경될 때 노드의 차수정보가 변경되면 edge가 삭제 되는 방식은 잘못된 Modularity를 계산할 수 있기에 서브 그래프 내의 차수변화를 정확히 반영한 모듈러리티 계산이 가능해진다.
\(Q_g = s^T B^{(g)} s\) 서브그래프 또한 마찬가지로 modularity를 동일하게 정의해줍니다. 이때 s는 서브그래프 내에서 노드의 커뮤니티 정보를 나타내며, $Q_g$는 서브그래프 g가 전체 모듈러리티에 기여하는 값을 나타냅니다. 만약 서브그래프를 나누지 않는다면 해당 modularity는 0으로 불필요한 커뮤니티 분할을 하지 않게 해준다.
만약 네트워크가 완벽하다면, 즉 모든 노드가 연결되어있다면 이를 complete network라 하며 $k_i^{(g)} \rightarrow k_i, \quad d_g \rightarrow 2m$ 다음과 같이 바꿀 수 있게 되며 이는 위의 식 2번과 똑같은 형태가 됩니다.
그렇다면 해당 방법을 통해 네트워크를 분할 할 때 언제 분할을 멈춰야할까? 잘못된 시점에 분할을 멈추면 불필요한 분할이 발생하거나 커뮤니티 구조를 놓칠 수 있다. 그래서 해당 논문에서는 $Q_g > 0$ 일때만 분할을 해야한다고 한다. 왜냐하면 서브그래프 g가 modularity를 증가시키는지 여부를 판단하면 되기 때문이다.
이때도 마찬가지로 $B^{(g)}$의 leading eigenvalue(가장 큰 고유값)을 확인한다. 이때 해당 값이 0이하라면 더이상 분할 할 필요가 없다는 것이다. 여기서 더이상 나눌 필요 없다는 서브그래프를 indivisible 상태라 한다.
근데 여기서 모든 고유값이 0이면 indivisible 상태지만, 정말 작은 양의 eigenvalue가 존재하고 정말 큰 음의eigenvalue가 존재하면 음수의 기여가 더 커서 전체 modularity가 될 수 있어 이경우에도 분할을 멈춰야한다. 이를 처리하는 방법은 간단하지만 해당 논문에서는 계산 효율을 위해 modularity가 0보다 큰지만 확인한다고 한다.
그래서 지금까지의 알고리즘을 요약하면 다음과 같다.
- 초기 네트워크에 Modularity Matrix B 계산
- 가장 큰 eigenvalue와 eigenvactor 계산
- eigenvactor의 요소들을 부호를 기준으로 두부분으로 나눔
- 각 서브 그래프에 동일한 과정 반복
- 서브그래프에 moudarity matrix 계산
- 가장 큰 eigenvalue를 확인해 0이하면 그래프를 분할하지 않음
- 양의 eigenvalue가 있어도 modularity 값이 0이하라면 분할을 멈춤
- 모든 서브 그래프가 Indivisible 상태가 되면 알고리즘 종료
Further techniques for modularity maximization
이제 Modularity가 어떻게 계산되고 어떤 알고리즘에 의해 작동되는지 알아봤으니 modularity를 최적화하는 방법에 대해 알아보자. 기존의 spectral method와는 완전히 다른 kernighan-Lin 알고리즘에 기반한 방법이다.
일단 해당 알고리즘은 다음과 같이 작동된다. 우선 모든 vertices를 하나의 그룹에 넣고 다른 그룹은 비워둔다. 그 상태에서 한개의 노드를 다른 그룹으로 이동시키고 modularity 증가량을 계산한다. 이때 모든 노드가 가장 많이 증가하는 경우를 찾고, 만약 모든 노드가 modularity 감소량을 가진다면 가장 작은 감소를 하는 이동을 선택한다. 이러한 이동을 모든 노드가 한번씩 이동할까지 반복한다. (이때 각 노드는 한번씩만 이동할 수 있다는 제한을 걸어둔다). 만약 모든 노드의 이동이 완료되면 알고리즘이 지나온 중간상태 intermediate states를 검토해 각 상태의 modularity를 평가해 가장 높은 modularity를 갖는 상태를 찾는다.
그리고 해당 방법은 spectral method와 결합해서 modularity를 극대화 시킬 수 있다. 처음에 위에서 언급한 그래프 라플라시안 방법을 통해서는 graph partitoning하는 task를 할 수 있습니다. spectral partitioning으로 네트워크를 처음에 두 부분으로 나누는 초기 분할에 사용합니다. 그리고 그 후에 위에 언급한 KL 알고리즘을 통해 refine하는 방법을 사용합니다. community detection에서도 그래프 분할과 같은 방식으로 작동하며 좋은 성과를 보인다고 합니다.
이제 최종적인 알고리즘 작동방식을 정리해봅시다.
- Modularity Matrix의 가장큰 eigenvalue와 eigenvactor를 계산하고 네트워크를 2개의 커뮤니티로 분할
- 그 이후 vertex moving method(KL 알고리즘)을 통해 모든 노드를 평가해 모듈러리티를 최대화 할 수 있는 방향으로 노드하나를 이동시키며 모든 서브그래프가 indivisible 상태가 될때까지 반복
Example applications
해당 논문에서 제시한 알고리즘을 기존의 알고리즘과 비교하여 실험을 진행하였다.
정량적인 방법으로 평가하기 위해 Duch와 Arenas의 연구에서 수행한 방법을 통해 modularity를 비교합니다. 이때 위에 나온 연구에 등장한 총 6개의 데이터 셋을 통해 성능을 평가합니다.
비교 알고리즘
- Girvan and Newman (GN) : betweenness centrality를 사용해 커뮤니티 간 edge를 제거함
- Clauset, Newman, and Moore (CNM) : 그리디 알고리즘을 통해 최적화 사용
- Duch and Arenas (DA) : Extermal Optimization 방법을 사용
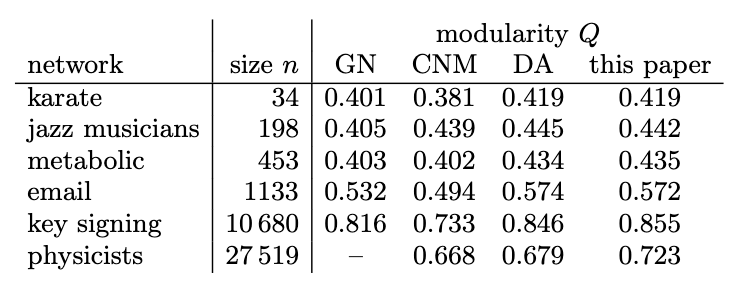
위 표를 보면 6개의 데이터셋에 대해 4가지 알고리즘을 서로 비교하고 있다. 그리고 눈여겨봐야할 점은 네트워크의 크기에 따른 성능 변화이다.
제일 먼저 논문에서 제시된 알고리즘은 모든 네트워크에서 GN과 CNM 알고리즘을 능가한다.
하지만 DA 알고리즘과 비교하면 조금 말이 다른데 작은 네트워크에서는 제시된 알고리즘과 DA 알고리즘의 성능차이가 거의 존재하지 않는다. 하지만 큰 네트워크에서는 DA 알고리즘보다 훨씬 좋은 성능을 보이는 것을 보이며 네트워크가 커질 수록 성능차이가 커지는 것을 알 수 있고 큰 네트워크에서는 6%의 성능 차이가 나는 것을 볼 수 있다.
또한 해당 표에 있는 modularity value는 알고리즘의 성공여부를 판단할 수 있는 정량적인 지표로 볼 수 있음을 알 수 있다. 이를 통해 real world problem에 이를 적용했을 때 합리적인 결과를 제공함을 보장할 수 있다. 실제로 위 Fig2에서 언급된 카라테 클럽 네트워크에서 현실 상황과 일치한 결과를 보여주었다.
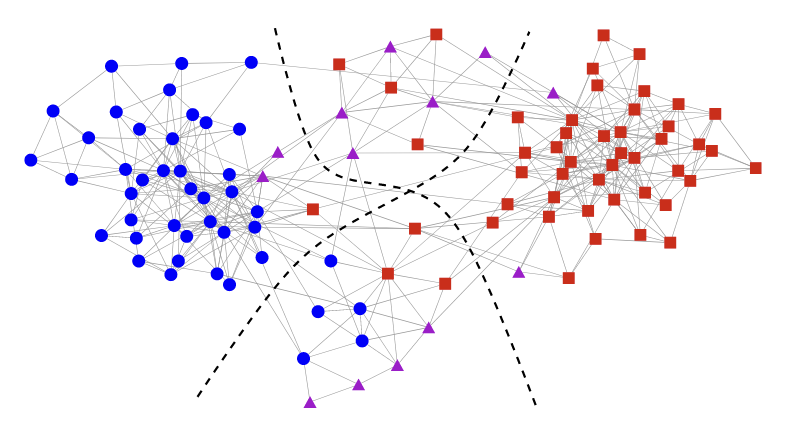
다음 figure는 실제로 정치관련 서적 네트워크를 활용해 community detection을 수행한 실제 사례에 대해 설명한다.
해당 네트워크는 V. Krebs에 의해 수집된 미국 정치관련 서적 데이터이며 105개의 서적이 노드로, 같은 구매자가 함께 구매한 서적의 쌍이 edge로 연결된다. 즉 관련성 있는 책들이 연결되며, 구매자의 정치적 성향이 반영될 가능성이 높다고 볼 수 있다.
그래서 해당 네트워크에 커뮤니티를 detection한 결과 위 figure처럼 결과가 나오게 되었다. 알고리즘은 총 4개의 커뮤니티를 감지했으며, 자유주의 서적, 보수주의 서적 그리고 중도적 서적 2편으로 네트워크가 구성되었다. 이를 통해 알고리즘이 원시 네트워크 데이터에서 의미 있는 결과를 도출할 수 있다는 것을 알 수 있다. 또한 중도적인 서적들이 독립적인 커뮤니티를 구성하며, 이는 정치적으로 양극화 되는 것이 아닌 중도층도 의미있는 커뮤니티를 가진다는 것을 시사한다.
두번째 예시로 정치 블로그 네트워크의 알고리즘 평가 사례를 언급하고 있다. 해당 네트워크에서는 노드 1225개가 각각의 블로그를, 그리고 두 블로그 사이의 하이퍼링크를 edge로 나타냈다. 해당 네트워크에 알고리즘을 적용한 결과 두개의 커뮤니티로 나누는 분할을 됐다. 분할결과 보수주의 블로그는 97%가 보수주의 였고, 자유주의는 93%가 자유주의로 나누어졌다. 또한 해당 알고리즘이 indivisible 상태가 되어 더 이상 커뮤니티를 분할 하지 않았다고 한다.
마지막으로 해당 알고리즘의 시간 복잡도에 대해 언급하고 있다. 해당 알고리즘의 시간 복잡도는 $O(n^2 \log n)$로 n은 노드수를 나타낸다. 다른 알고리즘의 경우 위에 언급된 순서대로 $O(n^3), O(n \log^2 n), O(n^2 \log^2 n)$이다. 이때 CNM 알고리즘을 빼곤 다 해당 알고리즘 보다 느린 속도이고, CNM 알고리즘은 시간복잡도는 더 빠르지만 커뮤니티 감지 결과가 더 좋지 않다. 2006년 PC로 노드 약 10만개까지 합리적으로 처리 가능하고, 27000개의 노드 네트워크를 해당 알고리즘은 20분 정도에 계산할 수 있었다.
Conclusions
- 해당 논문에서는 Modularity Matrix의 eigenvalue와 eigenvactor를 이용한 새로운 커뮤니티 감지 알고리즘을 개발하였다.
- 기존의 알고리즘과 비교했을때 더 나은 성능과 실행 속도 측면에서 더 좋은 성능을 보였다.
- 실세계 데이터에 적용을 했을때 합리적인 커뮤니티 분할을 제공했으며, modularity value 측면에서도 좋은 성능을 보였다.