일단 적고보자

ACM 2024. [Paper]
David Y. Kang, Qiaozhu Mei, Sang-Wook Kim
University of Michigan, Hanyang University
13 May 2024

Introduction

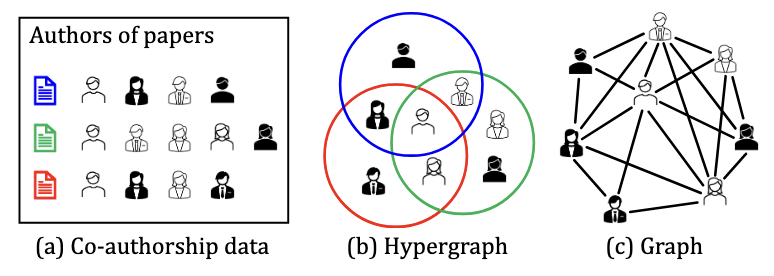
그래프는 다양한 분야에서 활용되고 있지만 실제 세계의 관계를 완벽하게 표현하지 못한다. 실제로 현실 세계는 하나 이상의 관계를 갖는 경우가 많다. 그렇기 때문에 기존의 그래프만으로 세상을 표현하는데 어려움이 있기에 하이퍼 그래프를 사용한다. 하이퍼그래프는 기존의 edge 대신 hyperedge를 통해 여러 노드간의 관계를 연관시켜 tuplewise 관계를 나타낼 수 있다.

위의 figure는 3개의 논문이 있을때 참여한 사람이 중복해서 있는 경우를 보여준다. 이를 hypergraph의 형태로 나타내면 (b)와 같은 형태로, 같은 논문에 참여한 사람끼리 하나의 원으로 묶어서 표현할 수 있다. (c)의 경우 일반 그래프로 표현한 것인데 이 경우 관계가 있는 사람끼리 모두 edge로 연결되며, 어떤 논문을 같이 참여했는지 확인하지 못하고 다른 사람과 협력을 했는지 여부만 알 수 있게 된다.

위와 같은 이유로 hypergraph는 실생활에서 다양한 형태로 활용된다.(ex. 추천시스템) hypergraph가 graph에 비해 우수한 성능을 보이기에 hypergraph를 graph로 확장하여 이를 딥러닝과 함께 사용하는데, 이를 hypergraph expansion이라고 한다. hypergraph expansion을 하는 이유는 그래프의 경우 hypergraph에 비해 다루기 좋은 다양한 알고리즘이 이미 많기 때문이다. 그리고 hypergraph expansion을 하는 방법에 대한 연구는 많이 진행되었지만, 어떤 hypergraph expansion이 더 좋은지에 대한 연구는 많이 진행되지 않았다. 그래서 해당 논문에서는 어떤 hypergraph expansion이 더 좋은지를 판단하는 방법을 제안한다.

Hypergraph Expansion Method

hypergraph expansion은 총 4가지 방법이 존재한다.

  • clique expansion(C) : 가장 직관적인 방법으로 만약 같은 hyperedge에 속하는 노드끼리 다 연결해주는 방법이다.
  • star expansion(S) : 기존의 node(n-node)는 유지한채로 각 hyperedge에 해당하는 노드(h-node)를 추가한다. 그리고 각 hyperedge에 해당하는 노드와 hyperedge를 선으로 연결해준다.
  • multi-level decomposition(M) : 이는 노드를 단계별로 그래프를 만드는 방법이다. level 1의 경우 clique과 동일하다. 하지만 level 2에서는 같은 Hyperedge내의 두 노드 쌍을 하나의 node로 보고 그래프를 형성한다. 그리고 같은 hyperedge 내에 있는 노드끼리 연결해준다. level3부터도 마찬가지다
  • linear expansion(L) : Linear expansion의 경우 직관적이진 않지만, 다음과 같은 방법을 통해 그래프가 만들어진다. 먼저 노드의 경우 hypergraph의 node와 hyperedge의 조합으로 만든다. 그리고 다음 2가지의 경우 노드끼리 연결한다. 1. 같은 하이퍼 그래프에 속한 노드인 경우 2. 실제로 같은 노드인 경우
  • combining clique and star expansion(CS) : 해당 논문에서 제안하는 방법이다. 기존 star expansion에서 노드 부분에 각 노드간의 관계를 clique expansion으로 연결해준 관계이다.

Downstream작업은 위의 hyper expansion 기법들을 통해 이뤄진다. 하지만 머신러닝에서는 어떤 기법을 사용할지 비교 분석을 사용하는 것과 달리, 타 연구에서는 해당 기법들을 별다른 분석 없이 선택을 하고 있다. 하지만 해당 기법들중 뭐가 더 나은지에 대한 정답은 없으며 경험에 기반해 선택된다. 그래서 해당 논문에서는 hypergraph expansion을 비교분석을 진행하였다.

Information Loss in Hypergraph Expansion

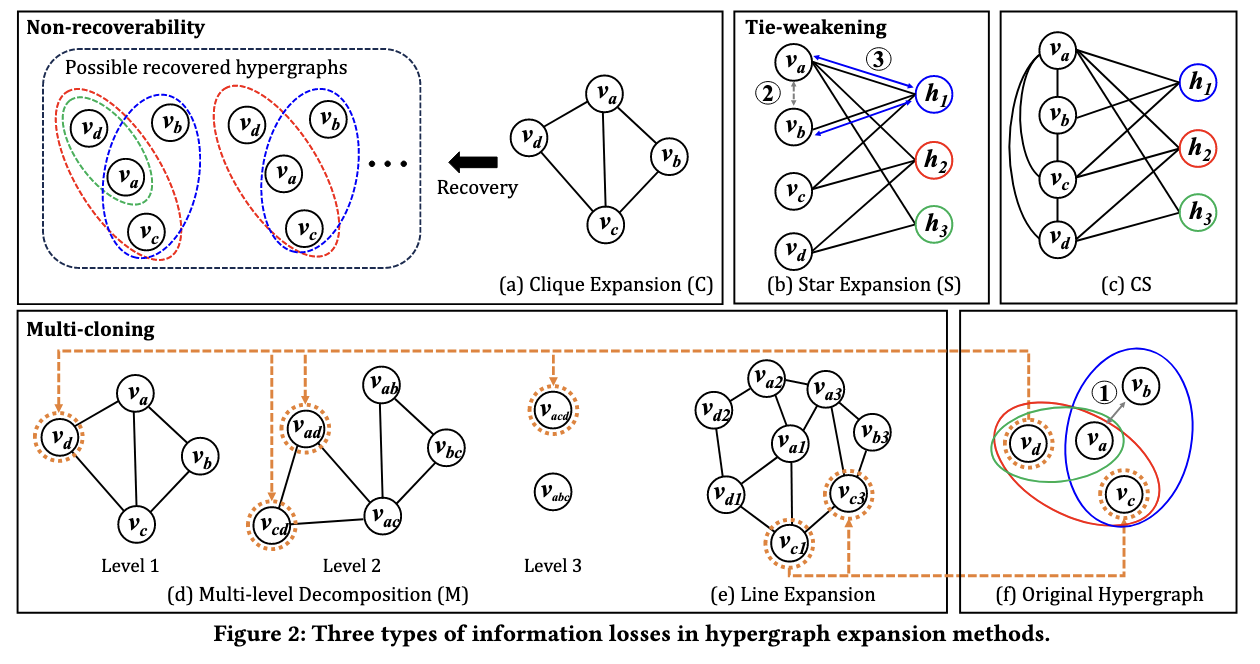
여기서 저자는 hypergraph expansion에서 모든 tuplewise관계를 pairwise 관계로 변환시킨다. 해당 과정에서 원래 hypergraph의 정보에 손실이 발생할 수 있고, downstream 작업의정확도를 떨어트린다. 그래서 이런 문제를 hypergraph expansion에서의 information loss라 정의한다. 또한 information loss를 3가지 타입으로 분류한다.

  • non-recoverability : expanded graph에서 원래의 hypergraph를 복원할 수 없는 문제
  • tie-weakening : 같은 hyperedge로 부터 나온 노드끼리의 연결 정도가 expanded graph에서 더 약해지는 문제
  • multi-cloning : 원래 하나였던 노드가 expaned graph가 되면서 여러개의 노드로 표현되는 문제

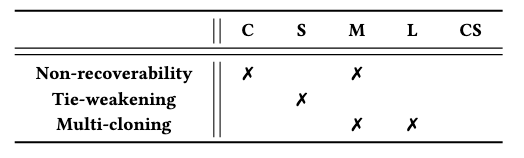
그리고 각 hypergraph expansion method에서 발생할 수 있는 Information Loss는 위 표와 같다.

MILEAGE: THE PROPOSED FRAMEWORK

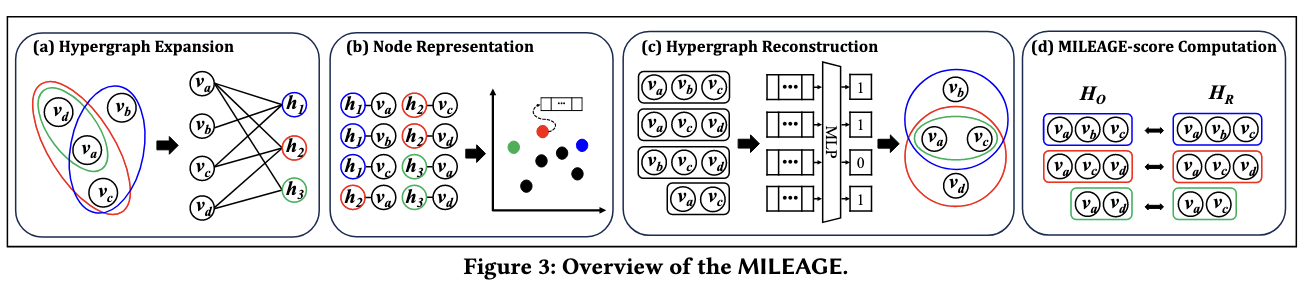
제안된 MILEAGE 프레임워크는 다음 figure와 같다. 여기서 MILEAGE는 information lossd의 정도를 나타낸다고 보면 된다. 제일먼저 기존의 hypergraph를 hyper graph expansion 방법을 통해 graph로 변환 한다. 그다음 노드를 URL(Unsupervised representation learning)을 통해 노드를 저차원 벡터로 임베딩한다. 다음은 Hypergraph reconstruction으로 임베딩된 벡터를 이용하여 원래의 hypergraph를 복구시킨다.

해당 과정에서는 기존 hypergraph에서 h개의 hyperedge를 추출하고(positive hyperedge), h개의 negative hyperedge도 추출한다. 이때 negative hyperedge는 Clique Negative Sapling기법을 사용하는데 해당 방법은 기존의 positive hyperedge에서 랜덤 노드를 변경하여 만든다. 그렇게 되면 총 2h개의 hyperedge가 만들어진다. 해당 hyperedge를 heuristic based prediction과 model based prediction으로 해당 hyperedge에 대한 분류를 진행한다.

\[\mathbf{x}_{hea} = \frac{1}{|\text{he}_a|C_2} \sum_{i,j \in \text{he}_a, j>i} \text{sim}(\theta_{vj}, \theta_{vi}),\]

먼저 휴리스틱한 방법으로 hyperedge를 분류하는 방법이다. 해당 수식을 보면 $\text{he}a$는 hyperedge를 그리고 $\theta{vj}$와 $\theta_{vi}$는 그 hyperedge 안의 노드의 벡터를 의미한다. 여기서 sim연산은 유사도를 측정하는 것을 의미하는데 여기서는 dot product 즉 내적을 이용하였다. 여기서 수식으로 나오는 결과는 해당 hyperedge의 positiveness 즉 해당 hyperedge가 얼마나 positive hyperedge에 가까운지 수치로 나오게 된다.

\[\theta_{hea} = \frac{1}{|\text{he}_2|C}_2 \sum_{i,j \in \text{he}_a, j>i} (\theta_{vj} - \theta_{vi}),\]

다음은 모델 기반의 hyperedge를 구하는 방법이다. 아까와 다른 점은 두 노드의 임베딩 벡터를 빼서 나온 벡터를 모델에 넣어 학습시키는 방법이다. 해당 방법의 경우 MLP를 사용하였다고 한다.

\[\text{mileage}(H_o, H_r) = 1 - \text{precision} = 1 - \frac{|H_o \cap H_r|}{|H_r|}.\]

다음은 MILAGE 점수를 계산하는 과정이다. 해당 과정은 다음과 같은 수식으로 계산 된다. $H_o, H_r$의 경우 hyperedge의 set을 의미한다. 의 경우 재구성된 HyperGraph가 기존의 HyperGraph와 얼마나 겹치는지를 통해 계산된다. 해당 점수는 Information Loss를 나타내므로 낮을 수록 잘 Reconstruction이 진행되었다고 보면 된다.

Experiment

해당 논문에서는 총 5가지의 평가 질문을 다루고 있다.

  • EQ1: 정보 손실과 다운스트림 작업 정확도 간의 관계 분석
  • EQ2: MILEAGE가 특정 URL 방법에 의존하지 않는지 검증
  • EQ3: 정보 손실이 가장 적은 하이퍼그래프 확장 방법 찾기
  • EQ4: MILEAGE가 네거티브 샘플링 방법의 영향을 받지 않는지 검증
  • EQ5: MILEAGE의 파라미터가 실험 결과에 미치는 영향 분석

EQ1 & EQ2

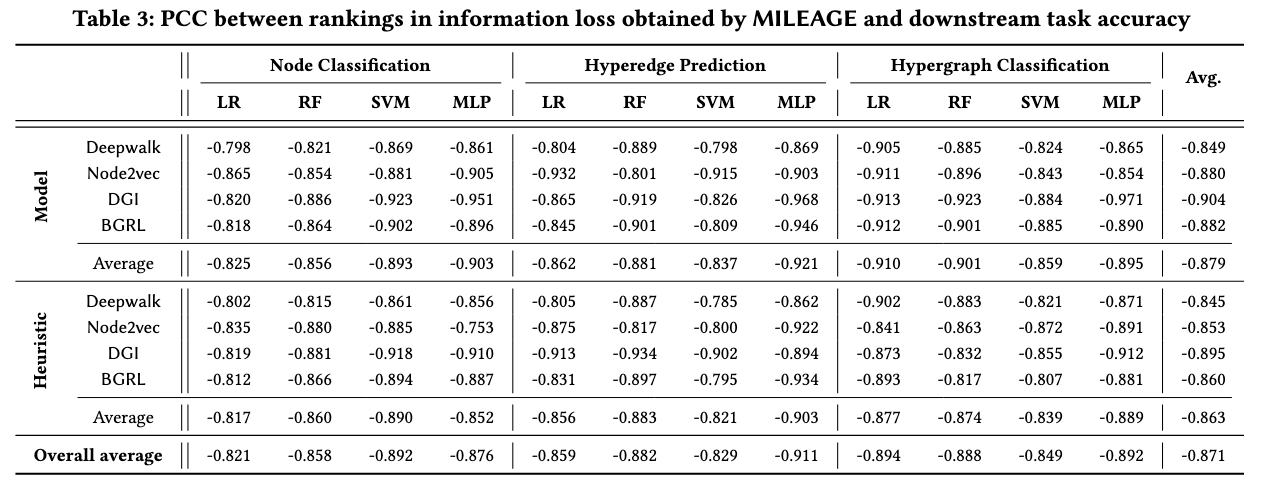
해당 논문에서는 총 8가지의 데이터셋을 통해 실험을 진행하였다. MILEAGE가 downstream 작업간의 피아손 상관 분석(Pearson correlation coefficient (PCC))을 진행한다. 상관관계를 파악하므로 절대값이 1에 가까울수록 좋고, 0에 가까울수록 안좋다. 우선 여기서 4가지 방법의 URL기법을 사용하였다 Deepwalk, Node2vec, DGI , BGRL. 해당 방법을 볼 경우 모든 방법을 했을 때 평균 -0.871 최소값 -0.904로 굉장히 좋은 결과를 보여준다. 여기서 DGI를 통한 URL기법이 가장 좋은 성능을 보임을 알 수 있다. 또한 3가지의 작업에서 휴리스틱 방법보다 모델기반 방법이 더 좋은 성능을 보임을 알 수 있다.

해당 결과를 통해 알 수 있는 점은 다음과 같다.

  1. information loss문제는 downstream 작업에서 안좋은 영향을 미친다.
  2. MILEAGE는 URL 방식에 영향을 받지 않고 측정할 수 있다.
  3. MILEAGE는 Hypergraph Expansion Method를 적절하게 평가할 수 있다.

EQ3

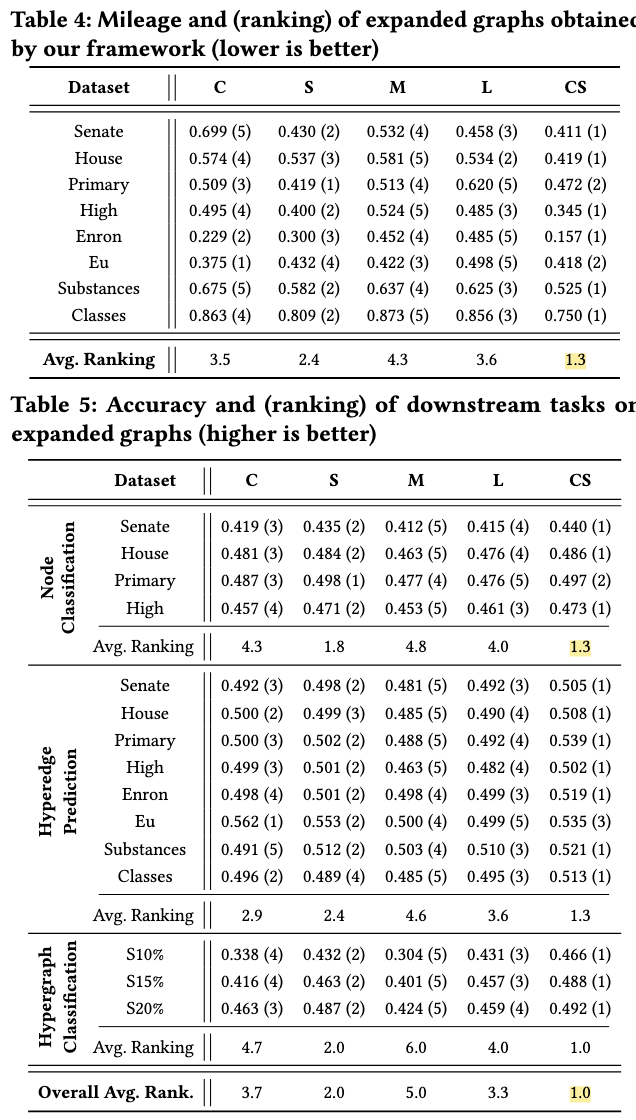
downsteam task를 DGI와 MLP를 이용하여 hypergraph expansion을 할때 어떤 방법이가장 효율적인지를 실험하였다.그 결과 CS가 가장 낮은 mileage(information loss)를 보여주었다.

EQ4

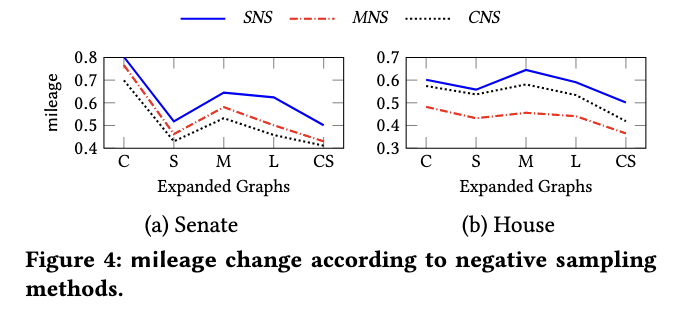
MILEAGE가 Negative sapling 방식에 따라 다르게 나오는지에 대한 실험도 진행하였다. 여기서는 총 3가지의 Negative sampling을 2가지 데이터셋에 적용시켰다. 그 결과 다양한 Negative Sampling방법에 대해 일관적인 모습을 볼 수 있었다.

EQ5

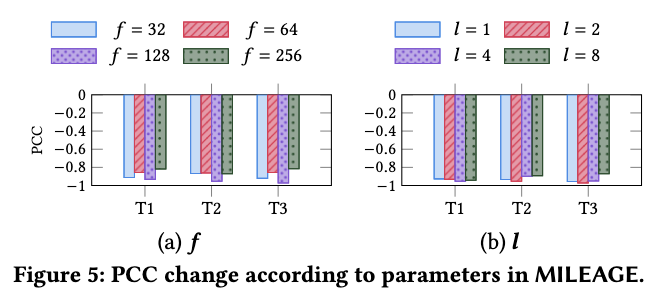
마지막으로 파라미터에 따른 Mileage의 민감도이다. 여기서는 총 2가지 파라미터에 대해 실험을 진행한다. 첫번째는 PCC를 진행할때 차원의 수(f)의 변화에 따른 mileage변화이다. 여기서는 32, 64, 128, 그리고 256의 변화를 주었으며 T1,T2,T3는 총 3가지 작업(node classification (NC), hyperedge prediction (HP), and hypergraph classification (HC)))에 대한 것을 의미한다. 그 결과 f에 대해서는 일관적인 모습을 보여주며 f의 값에 민감하게 반응하지 않음을 알 수 있다.

다음은 레이어 수를 변화함에 따라 변화를 관찰하였다. 그결과 layer수가 2가 될때까지는 감소하다가 그 이후로는 증가하는 모습을 보였다. 이 수치는 레이어 변화에 따라 변화가 크지 않기때문에, Mileage는 레이어의 수에도 둔감하지 않다는 것을 알 수 있다.

You may also enjoy